【题目】等腰直角![]() 和等腰直角
和等腰直角![]() 分别在直线
分别在直线![]() 上.
上.
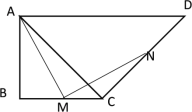
(1)如图所示,![]() 分别在线段
分别在线段![]() 上,若
上,若![]() ,求证:
,求证:![]() .
.
(2)若![]() 分别在线段
分别在线段![]() 外(还在直线
外(还在直线![]() 上),根据题意,画出图形,那么(1)的结论是否依然成立,若成立,写出证明过程;若不成立,说明原因;
上),根据题意,画出图形,那么(1)的结论是否依然成立,若成立,写出证明过程;若不成立,说明原因;
(3)如图,若![]() ,求证:
,求证:![]() .
.

参考答案:
【答案】(1)详见解析;(2)成立,详见解析;(3)详见解析
【解析】
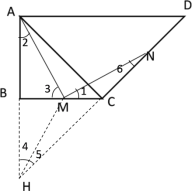
(1)延长![]() ,交
,交![]() 的延长线于
的延长线于![]() ,连接
,连接![]() ,先证出△BHC为等腰直角三角形,然后证出BC是
,先证出△BHC为等腰直角三角形,然后证出BC是![]() 的垂直平分线,根据垂直平分线的性质可得
的垂直平分线,根据垂直平分线的性质可得![]() ,然后根据等边对等角和等角对等边证出HM=MN,即可证出结论;
,然后根据等边对等角和等角对等边证出HM=MN,即可证出结论;
(2)根据题意,分点M在CB的延长线和点M在BC的延长线两种情况讨论,分别画出对应的图形,根据垂直平分线的性质、等边对等角和等角对等边分别证明即可;
(3)延长![]() ,交
,交![]() 的延长线于
的延长线于![]() ,连接
,连接![]() ,由(1)可得
,由(1)可得![]() 是
是![]() 的垂直平分线,然后根据等边对等角和等量代换即可证出
的垂直平分线,然后根据等边对等角和等量代换即可证出![]() ,从而证出结论.
,从而证出结论.
解:(1)延长![]() ,交
,交![]() 的延长线于
的延长线于![]() ,连接
,连接![]() .
.
![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]()
∵等腰直角![]() 和等腰直角
和等腰直角![]()
![]() ,
,
![]() ,
,
![]() 为等腰直角三角形,
为等腰直角三角形,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() 是
是![]() 的垂直平分线,
的垂直平分线,
![]() ,
,
![]() ,
,
![]() ,
,
而![]() ,
,
![]()
![]() ,
,
![]()
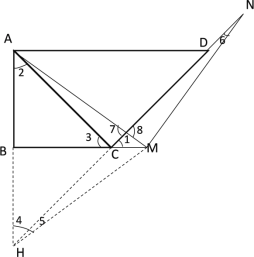
(2)成立,证明如下
第一种情况:如图所示
延长![]() ,交
,交![]() 的延长线于
的延长线于![]() ,连接
,连接![]() ;
;
由(1)可得:![]() ,
,![]() ,
,
![]() ,
,
显然![]() 是
是![]() 的垂直平分线,
的垂直平分线,
![]()
![]() ,且
,且![]() ;
;
![]() ,
,
![]() ,
,
![]()

第二种情况:
易证显然![]() 是
是![]() 的垂直平分线,
的垂直平分线,
![]()
![]() ,
,
即![]() ,
,
![]()
而![]() ,∠7=∠8,
,∠7=∠8,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
(3)延长![]() ,交
,交![]() 的延长线于
的延长线于![]() ,连接
,连接![]() .
.
由(1)可得![]() 是
是![]() 的垂直平分线,
的垂直平分线,
![]() ,
,
∴![]()
而![]() ,
,
![]() ,
,
又![]() ,
,
![]()
而![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.

(1)求证:△AEC≌△ADB;(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分8分)某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求.商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润率不低于25%(不考虑其它因素),那么每件衬衫的标价至少是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数
 的图象交
的图象交 轴于
轴于 两点,交
两点,交 轴于点
轴于点 ,点
,点 的坐标为
的坐标为 ,顶点
,顶点 的坐标为
的坐标为 .
.
(1)求二次函数的解析式和直线
 的解析式;
的解析式;(2)点
 是直线
是直线 上的一个动点,过点
上的一个动点,过点 作
作 轴的垂线,交抛物线于点
轴的垂线,交抛物线于点 ,当点
,当点 在第一象限时,求线段
在第一象限时,求线段 长度的最大值;
长度的最大值;(3)在抛物线上是否存在异于
 的点
的点 ,使
,使 中
中 边上的高为
边上的高为 ,若存在求出点
,若存在求出点 的坐标;若不存在请说明理由.
的坐标;若不存在请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l和双曲线y=
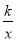 (k>0)交于A、B两点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别为C、D、E,连接OA、OB、OP,设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3,则( )
(k>0)交于A、B两点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别为C、D、E,连接OA、OB、OP,设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3,则( )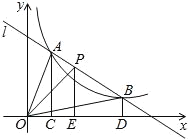
A.S1<S2<S3B.S1>S2>S3C.S1=S2>S3D.S1=S2<S3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图中实线所示,函数y=|a(x﹣1)2﹣1|的图象经过原点,小明同学研究得出下面结论:
①a=1;②若函数y随x的增大而减小,则x的取值范围一定是x<0;
③若方程|a(x﹣1)2﹣1|=k有两个实数解,则k的取值范围是k>1;
④若M(m1,n),N(m2,n),P(m3,n),Q(m4,n)(n>0)是上述函数图象的四个不同点,且m1<m2<m3<m4,则有m2+m3﹣m1=m4.其中正确的结论有( )

A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】有专家指出:人为型空气污染(如汽车尾气排放等)是雾霾天气的重要成因.某校为倡议“每人少开一天车,共建绿色家园”,想了解学生上学的交通方式.九年级(8)班的5名同学联合设计了一份调查问卷.对该校部分学生进行了随机调查.按A(骑自行车)、B(乘公交车)、C(步行)、D(乘私家车)、E(其他方式)设置选项,要求被调查同学从中单选.并将调查结果绘制成条形统计图1和扇形统计图2,根据以上信息,解答下列问题:
(1)本次接受调查的总人数是 人,扇形统计图中“骑自行车”所在扇形的圆心角度数是 度,请补全条形统计图;
(2)已知这5名学生中有2名女同学,要从这5名学生中任选两名同学汇报调查结果.请用列表法或画树状图的方法,求出恰好选出1名男生和1名女生的概率.

相关试题

