【题目】已知:如图,在ABCD中,点E是BC的中点,连接AE并延长交DC的延长线于点F,连接BF.
(1)求证:△ABE≌△FCE;
(2)若AF=AD,求证:四边形ABFC是矩形.

参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)根据平行四边形性质得出AB∥DC,推出∠1=∠2,根据AAS证两三角形全等即可;
(2)根据全等得出AB=CF,根据AB∥CF得出平行四边形ABFC,推出BC=AF,根据矩形的判定推出即可.
(1)如图.
∵四边形ABCD是平行四边形,
∴AB∥DC 即 AB∥DF,
∴∠1=∠2,
∵点E是BC的中点,
∴BE=CE.
在△ABE和△FCE中,
 ,
,
∴△ABE≌△FCE(AAS).
(2)∵△ABE≌△FCE,
∴AB=FC,
∵AB∥FC,
∴四边形ABFC是平行四边形,
∴AD=BC,
∵AF=AD,
∴AF=BC,
∴四边形ABFC是矩形.
-
科目: 来源: 题型:
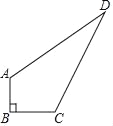
查看答案和解析>>【题目】某中学有一块四边形的空地ABCD,如图所示,学校计划在空地上种植草皮,经测量∠B=90°,AB=3m,BC=4m,CD=12m,AD=13m.若每平方米草皮需要200元,问学校需要投入多少资金买草皮?
-
科目: 来源: 题型:
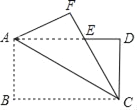
查看答案和解析>>【题目】如图,将长方形ABCD沿对角线AC翻折,点B落在点F处,FC交AD于点E,若AB=4,BC=8,则△ACE的面积为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 ,
, 之间有一条曲线和一条线段,
之间有一条曲线和一条线段,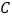 在线段
在线段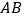 上,己知
上,己知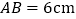 ,
,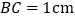 ,
,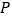 是线段
是线段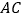 上一动点,过点
上一动点,过点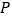 作
作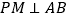 交曲线于点
交曲线于点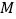 ,连接
,连接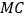 ,过点
,过点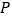 作
作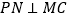 于点
于点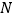 .设
.设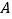 ,
,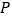 两点间的距离为
两点间的距离为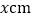 ,
,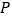 ,
,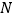 两点间的距离为
两点间的距离为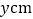 .(当点
.(当点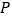 与点
与点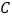 重合时,
重合时,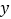 的值为
的值为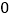 )小思根据学习函数的经验,对函数
)小思根据学习函数的经验,对函数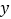 随自变量
随自变量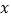 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.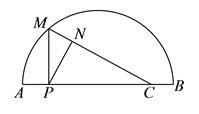
下面是小思的探究过程,请补充完整:
(
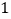 )通过取点,画图,测量,得到了
)通过取点,画图,测量,得到了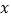 与
与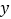 的几组值,补全下表:
的几组值,补全下表: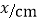
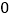
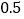
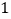
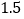
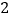
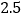
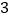
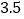
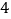

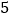
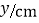
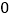
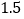
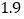
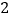
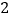
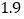
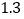
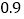
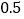
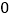
(说明:补全表格时相关数值保留一位小数)
(
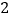 )在下列平面直角坐标系中描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.
)在下列平面直角坐标系中描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.
(
 )结合画出的函数图象,解决问题:当
)结合画出的函数图象,解决问题:当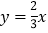 时,
时,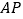 的长度约为__________
的长度约为__________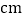 (结果保留一位小数).
(结果保留一位小数). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:ΔABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与CD相交于点O, ∠AOM=90°,

(1)如图1,若OC平分∠AOM.求∠AOD的度数;
(2)如图2,若∠BOC=4∠NOB,且OM平分∠NOC,求∠MON的度数;
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等边
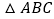 中,
中, ,点
,点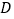 为
为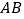 的中点,点
的中点,点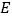 是
是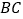 边上一动点,
边上一动点,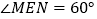 ,且
,且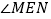 的两边分别与
的两边分别与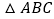 的边
的边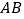 ,
,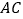 交于点
交于点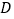 ,
,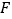 (点
(点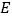 不与点
不与点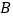 ,
,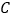 重合).
重合).(
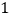 )当
)当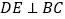 时,请在图
时,请在图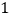 中补全图形.
中补全图形.(
 )在图
)在图 中,设
中,设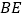 的长为
的长为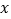 ,
,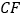 的长为
的长为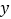 ,求
,求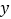 与
与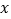 的函数关系式,并写出自变量
的函数关系式,并写出自变量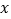 的取值范围.
的取值范围.(
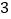 )如图
)如图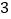 ,点
,点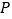 ,
,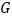 分别为
分别为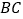 ,
,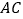 的中点,在
的中点,在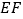 上截取
上截取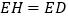 ,连接
,连接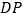 ,
,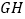 .请证明
.请证明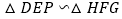 .
.
相关试题

