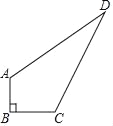
【题目】某中学有一块四边形的空地ABCD,如图所示,学校计划在空地上种植草皮,经测量∠B=90°,AB=3m,BC=4m,CD=12m,AD=13m.若每平方米草皮需要200元,问学校需要投入多少资金买草皮?
参考答案:
【答案】学校需要投入7200元买草皮.
【解析】
直接利用勾股定理的逆定理得出∠ACD=90°,再利用直角三角形的性质得出答案.
连接AC
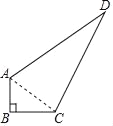
∵∠B=90°,AB=3m,BC=4m,BC=12m,
AC2=AB2+AD2=32+42=25,AC=5m,
∴AC2+CD2=25+144=169=132
又∵AD2=132,
∴AC2+CD2=CD2
∴∠ACD=90°,
∴△ACD是直角三角形,
∴四边形ABCD的面积=6+30=36(m2),
∴学校要投入资金为:200×36=7200(元);
答:学校需要投入7200元买草皮.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人相约元旦登山,甲、乙两人距地面的高度y(m)与登山时间x(min)之间的函数图像如图所示,根据图像所提供的信息解答下列问题:
(1)t= min.
(2)若乙提速后,乙登山的上升速度是甲登山的上升速度3倍,
①则甲登山的的上升速度是 m/min;
②请求出甲登山过程中,距地面的高度y(m)与登山时间x(min)之间的函数关系式.
③当甲、乙两人距地面高度差为70m时,求x的值(直接写出满足条件的x值).

-
科目: 来源: 题型:
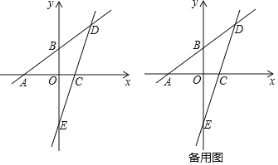
查看答案和解析>>【题目】已知:如图,一次函数y=
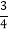 x+3的图象分别与x轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx+b的图象相交于点D,点D的横坐标为4,直线CD与y轴相交于点E.
x+3的图象分别与x轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx+b的图象相交于点D,点D的横坐标为4,直线CD与y轴相交于点E.(1)直线CD的函数表达式为______;(直接写出结果)
(2)在x轴上求一点P使△PAD为等腰三角形,直接写出所有满足条件的点P的坐标.
(3)若点Q为线段DE上的一个动点,连接BQ.点Q是否存在某个位置,将△BQD沿着直线BQ翻折,使得点D恰好落在直线AB下方的y轴上?若存在,求点Q的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )

A. AB∥CD,AD∥BC B. OA=OC,OB=OD C. AD=BC,AB∥CD D. AB=CD,AD=BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将长方形ABCD沿对角线AC翻折,点B落在点F处,FC交AD于点E,若AB=4,BC=8,则△ACE的面积为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 ,
, 之间有一条曲线和一条线段,
之间有一条曲线和一条线段, 在线段
在线段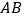 上,己知
上,己知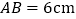 ,
,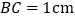 ,
,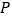 是线段
是线段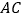 上一动点,过点
上一动点,过点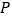 作
作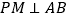 交曲线于点
交曲线于点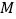 ,连接
,连接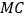 ,过点
,过点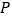 作
作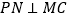 于点
于点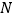 .设
.设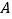 ,
,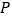 两点间的距离为
两点间的距离为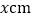 ,
,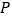 ,
,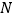 两点间的距离为
两点间的距离为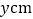 .(当点
.(当点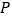 与点
与点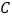 重合时,
重合时,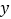 的值为
的值为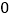 )小思根据学习函数的经验,对函数
)小思根据学习函数的经验,对函数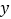 随自变量
随自变量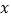 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.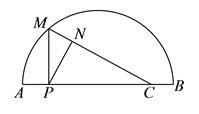
下面是小思的探究过程,请补充完整:
(
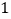 )通过取点,画图,测量,得到了
)通过取点,画图,测量,得到了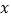 与
与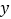 的几组值,补全下表:
的几组值,补全下表: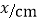
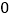
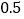
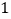
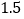
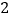
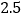
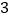
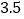
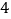

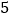
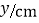
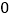
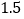
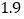
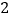
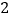
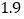
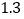
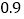
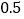
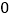
(说明:补全表格时相关数值保留一位小数)
(
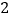 )在下列平面直角坐标系中描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.
)在下列平面直角坐标系中描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.
(
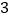 )结合画出的函数图象,解决问题:当
)结合画出的函数图象,解决问题:当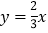 时,
时,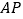 的长度约为__________
的长度约为__________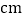 (结果保留一位小数).
(结果保留一位小数). -
科目: 来源: 题型:
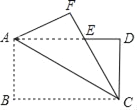
查看答案和解析>>【题目】已知:如图,在ABCD中,点E是BC的中点,连接AE并延长交DC的延长线于点F,连接BF.
(1)求证:△ABE≌△FCE;
(2)若AF=AD,求证:四边形ABFC是矩形.

相关试题

