【题目】已知△ABC中,AB=AC,BE平分∠ABC交边AC于E.
(1)如图(1),当∠BAC=108°时,证明:BC=AB+CE;
(2)如图(2),当∠BAC=100°时,(1)中的结论还成立吗?若不成立,是否有其他两条线段之和等于BC,若有请写出结论并完成证明.

参考答案:
【答案】(1)证明见解析;(2)BC=BE+AE,证明见解析.
【解析】
(1)如图1中,在BC上截取BD=BA.只要证明△BEA≌△BED,CE=CD即可解决问题;
(2)结论:BC=BE+AE.如图2中,在BA、BC上分别截取BF=BE,BH=BE.则△EBH≌△EBF,再证明EA=EH=EF=CF即可解决问题;
(1)如图1中,在BC上截取BD=BA.

∵BA=BD,∠EBA=∠EBD,BE=BE,
∴△BEA≌△BED,
∴BA=BD,∠A=∠BDE=108°,
∵AB=AC,
∴∠C=∠ABC=36°,∠EDC=72°,
∴∠CED=72°,
∴CE=CD,
∴BC=BD+CD=AB+CE.
(2)结论:BC=BE+AE.
理由:如图2中,在BA、BC上分别截取BF=BE,BH=BE.则△EBH≌△EBF,

∴EF=EH,
∵∠BAC=100°,AB=AC,
∴∠ABC=∠C=40°,
∴∠EBA=∠EBC=20°,
∴∠BFE=∠H=∠EAH=80°,
∴AE=EH,
∵∠BFE=∠C+∠FEC,
∴∠CEF=∠C=40°,
∴EF=CF,
∴BC=BF+CF=BE+AE.
-
科目: 来源: 题型:
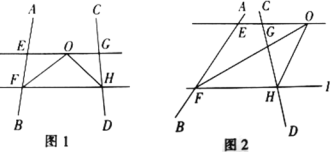
查看答案和解析>>【题目】[探究]如图,∠AFH和∠CHF的平分线交于点O,EG经过点O且平行于FH,分别与AB,CD交于点E、G.
(1)若∠AFH=60°,∠CHF=50°,则∠EOF= °,∠ FOH= °
(2)若∠AFH+∠CHF= 100°,求∠FOH的度数.
(3)当∠FOH=_____ °时 ,AB//CD.
[拓展]如图,∠AFH和∠CHI的平分线交于点O,EG经过点O且平行于FH,分别与AB,CD交于点E、G.若∠AFH+∠CHF=a,求∠FOH的度数. (用含a的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形网格中,小格的顶点叫做格点.三个顶点都在网格上的三角形叫做格点三角形.小华已在左边的正方形网格中作出了格点△ABC.请你在右边的两个正方形网格中各画出一个不同的格点三角形,使得三个网格中的格点三角形都相似(不包括全等).
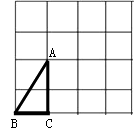

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在四边形ABCD中,
 ,延长BC至点E,连接AE交CD于点F,使
,延长BC至点E,连接AE交CD于点F,使
 求证:
求证:  ;
; 求证:
求证:  ;
;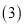 若BF平分
若BF平分 ,请写出
,请写出 与
与 的数量关系______
的数量关系______ 不需证明
不需证明

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位同学同解一道题目:“如图,F、G是直线AB上的两点,D是AC上的一点,且DF∥CB,∠E=∠C,请写出与△ABC相似的三角形,并加以证明”. 甲同学的解答得到了老师的好评.
乙同学的解答是这样的:“与△ABC相似的三角形只有△AFD,证明如下:
∵DF∥CB,
∴△AFD∽△ABC.”
乙同学的解答正确吗?若不正确,请你改正.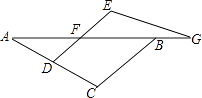
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年南方某地发生特大洪灾,政府为了尽快搭建板房安置灾民,给某厂下达了生产A种板材48000㎡和B种板材24000㎡的任务.
⑴如果该厂安排210人生产这两种材,每人每天能生产A种板材60㎡或B种板材40㎡,请问:应分
别安排多少人生产A种板材和B种板材,才能确保同时完成各自的生产任务?
⑵某灾民安置点计划用该厂生产的两种板材搭建甲、乙两种规格的板房共400间,已知建设一间甲型板房和一间乙型板房所需板材及安置人数如下表所示:
板房
A种板材(m2)
B种板材(m2)
安置人数
甲型
108
61
12
乙型
156
51
10
问这400间板房最多能安置多少灾民?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图△ABC中,D、E是AB、AC上点,AB=7.8,AD=3,AC=6,AE=3.9,试判断△ADE与△ABC是否会相似.

相关试题

