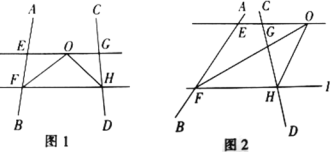
【题目】[探究]如图,∠AFH和∠CHF的平分线交于点O,EG经过点O且平行于FH,分别与AB,CD交于点E、G.
(1)若∠AFH=60°,∠CHF=50°,则∠EOF= °,∠ FOH= °
(2)若∠AFH+∠CHF= 100°,求∠FOH的度数.
(3)当∠FOH=_____ °时 ,AB//CD.
[拓展]如图,∠AFH和∠CHI的平分线交于点O,EG经过点O且平行于FH,分别与AB,CD交于点E、G.若∠AFH+∠CHF=a,求∠FOH的度数. (用含a的代数式表示)
参考答案:
【答案】(1)30,125;(2) 130°;(3)90°;拓展: 90°-![]() a.
a.
【解析】
(1)依据角平分线以及平行线的性质,即可得到∠EOF的度数,依据三角形内角和定理,即可得到∠FOH的度数;(2)依据角平分线以及平行线的性质、三角形内角和定理,即可得到∠FOH的度数; (3) 因为∠OFH=![]() ∠AFH,∠OHF=
∠AFH,∠OHF=![]() ∠CHF,所以∠OFH+∠CHF=
∠CHF,所以∠OFH+∠CHF=![]() (∠AFH+∠CHF),当∠AFH+∠CHF=180°时,AB//CD,此时 ∠OFH+∠CHF=
(∠AFH+∠CHF),当∠AFH+∠CHF=180°时,AB//CD,此时 ∠OFH+∠CHF=![]() (∠AFH+∠CHF)=
(∠AFH+∠CHF)=![]() ×180°=90° ,根据三角形内角和得:∠FOH=180°-(∠OFH+∠CHF )=90°.
×180°=90° ,根据三角形内角和得:∠FOH=180°-(∠OFH+∠CHF )=90°.
【拓展】根据∠AFH和∠CHI的平分线交于点O,可得∠OFH=![]() ∠AFH,∠OHI=
∠AFH,∠OHI=![]() ∠CHI,再根据∠FOH=∠OHI-∠OFH进行计算,即可得到∠FOH的度数.
∠CHI,再根据∠FOH=∠OHI-∠OFH进行计算,即可得到∠FOH的度数.
解,【探究】(1) )∵∠AFH=60°,OF平分∠AFH,
∴∠OFH=30°,
又∵EG∥FH,
∴∠EOF=∠OFH=30°;
∵∠CHF=50°,OH平分∠CHF,
∴∠FHO=25°,
∴△FOH中,∠FOH=180°-∠OFH-∠OHF=125°;
故答案为:30,125.
(2)因为FO平分∠AFH,HO平分∠CHF. 所以∠OFH=![]() ∠AFH,∠OHF=
∠AFH,∠OHF=![]() ∠CHF.
∠CHF.
因为∠AFH+∠CHF=100°,所以∠OFH+∠OHF=![]() (∠AFH+∠CHF)=50°
(∠AFH+∠CHF)=50°
∵EG∥FH,
∴∠EOF=∠OFH,∠GOH=∠OHF.
∴∠EOF+∠GOH=∠OFH+∠OHF=50°.
∵∠EOF+∠GOH+∠FOH=180°,
所以∠FOH= 180°-(∠OFH+∠OHF)=180°-50°![]() =130°.
=130°.
(3) ∵∠OFH=![]() ∠AFH,∠OHF=
∠AFH,∠OHF=![]() ∠CHF,
∠CHF,
∴∠OFH+∠CHF=![]() (∠AFH+∠CHF),
(∠AFH+∠CHF),
当∠AFH+∠CHF=180°时,AB//CD,此时 ∠OFH+∠CHF=![]() (∠AFH+∠CHF)=
(∠AFH+∠CHF)=![]() ×180°=90° ,根据三角形内角和得:∠FOH=180°-(∠OFH+∠CHF )=90°.
×180°=90° ,根据三角形内角和得:∠FOH=180°-(∠OFH+∠CHF )=90°.
【拓展】
因为∠AFH和∠CHI的平分线交干点O.
所以∠OFH=![]() ∠AFH,∠OHI=
∠AFH,∠OHI=![]() ∠CHI.
∠CHI.
因为EG//FH,所以∠EOH=∠OHI,∠EOF=∠OFH.
因为∠FOH=∠EOH-∠EOF,∠FOH=∠OHI-∠EOH=![]() (∠CHI-∠AFH)=90°-
(∠CHI-∠AFH)=90°-![]() a.
a.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC与△A'B'C'在平面直角坐标系中的位置如图所示
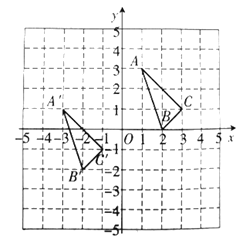
(1)分别写出下列各点的坐标:A_______ B_______ C_______
(2)△ABC由△A'B'C'经过怎样的平移得到?
(3)若点P(x,y)是△ABC内部点,则A'B'C' 内部的对应点P'的坐标为
(4)求△ABC的面积
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB≠AC.D、E分别为边AB、AC上的点.AC=3AD,AB=3AE,点F为BC边上一点,添加一个条件: , 可以使得△FDB与△ADE相似.(只需写出一个)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形网格上有6个三角形:①△ABC,②△CDB,③△DEB,④△FBG,⑤△HGF,⑥△EKF. 在②~⑥中,与①相似的三角形的个数是 .

-
科目: 来源: 题型:
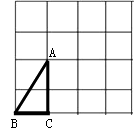
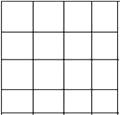
查看答案和解析>>【题目】正方形网格中,小格的顶点叫做格点.三个顶点都在网格上的三角形叫做格点三角形.小华已在左边的正方形网格中作出了格点△ABC.请你在右边的两个正方形网格中各画出一个不同的格点三角形,使得三个网格中的格点三角形都相似(不包括全等).

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在四边形ABCD中,
 ,延长BC至点E,连接AE交CD于点F,使
,延长BC至点E,连接AE交CD于点F,使
 求证:
求证:  ;
; 求证:
求证:  ;
;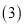 若BF平分
若BF平分 ,请写出
,请写出 与
与 的数量关系______
的数量关系______ 不需证明
不需证明

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,AB=AC,BE平分∠ABC交边AC于E.
(1)如图(1),当∠BAC=108°时,证明:BC=AB+CE;
(2)如图(2),当∠BAC=100°时,(1)中的结论还成立吗?若不成立,是否有其他两条线段之和等于BC,若有请写出结论并完成证明.

相关试题

