【题目】如图,已知线段AC为⊙O的直径,PA为⊙O的切线,切点为A,B为⊙O上一点,且BC∥PO.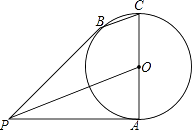
(1)求证:PB为⊙O的切线;
(2)若⊙O的半径为1,PA=3,求BC的长.
参考答案:
【答案】
(1)证明:连接OB,
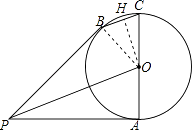
∵∠BCA= ![]() ,
,
又∵BC∥OP,
∴∠POA=∠BCA,
∴∠POA=∠BOP,
在△AOP与△BOP中, 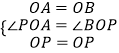 ,
,
∴△AOP≌△BOP,
∴∠PBO=∠PAO,
又∵PA为⊙O的切线,
∴∠PAO=90°,
∴∠OBP=90°,
又OB为⊙O的半径,
∴PB为⊙O的切线;
(2)解:过O作OH⊥BC于H,则CH= ![]() BC,
BC,

在Rt△AOP中,OP2=PA2+OA2=32+12=10,
又∵OP>0,
∴OP= ![]() ,
,
∵∠POA=∠BCA,
∴cos∠BCA=cos∠POA= ![]() ,
,
在Rt△OHC中,OC=1,cos∠BCA= ![]() 即
即 ![]() ,
,
∴CH= ![]() ,
,
∴BC=2CH= ![]() .
.
【解析】(1)要证PB为⊙O的切线,需要证明PB垂直于过B点的半径,为此连接OB,先证△AOP≌△BOP可得∠PBO=∠PAO,由题意可得∠PAO=90°,即可得证;
(2)连接AB,在Rt△AOP中由勾股定理可求得OP,易求得cos∠POA,又∠POA=∠BCA,可得cos∠BCA,在Rt△OHC中利用三角函数可求出CH,由BC=2CH可得.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有下列命题:①两条直线被第三条直线所截,同位角相等;②0.1的算术平方根是0.01;③算术平方根等于它本身的数是1;④如果点P(3-2n,1)到两坐标轴的距离相等,则n=1;⑤若a2=b2,则a=b;⑥若
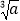 =
= ,则a=b.其中假命题的个数是( )
,则a=b.其中假命题的个数是( )A. 3个B. 4个C. 5个D. 6个
-
科目: 来源: 题型:
查看答案和解析>>【题目】“倡导全民阅读”、“推动国民素质和社会文明程度显著提高”已成为“十三五”时期的重要工作.教育主管部门对某学校青年学校青年教师2016年度阅读情况进行了问卷调查,并将收集的数据统计如表,根据表中的信息判断,下列结论错误的是( )

A. 该学校中参与调查的青年教师人数为40人
B. 该学校中青年教师2016年平均每人阅读8本书
C. 该学校中青年教师2016年度看书数量的中位数为4本
D. 该学校中青年教师2016年度看书数量的众数为4本
-
科目: 来源: 题型:
查看答案和解析>>【题目】如∠MON=30°、OP=6,点A、B分别在OM、ON上;(1)请在图中画出周长最小的△PAB(保留画图痕迹);(2)请求出(1)中△PAB的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为提高居民的节水意识,向阳小区开展了“建设节水型社区,保障用水安全”为主题的节水宣传活动,小莹同学积极参与小区的宣传活动,并对小区300户家庭用水情况进行了抽样调查,她在300户家庭中,随机调查了50户家庭5月份的用水量情况,结果如图所示.

(1)试估计该小区5月份用水量不高于12 t的户数占小区总户数的百分比;
(2)把图中每组用水量的值用该组的中间值(如0~6的中间值为3)来替代,估计该小区5月份的用水量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在平面直角坐标系中,二次函数y=﹣
 x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.
x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.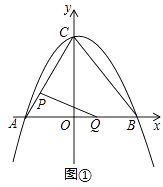
(1)填空:b= , c=;
(2)在点P,Q运动过程中,△APQ可能是直角三角形吗?请说明理由;
(3)在x轴下方,该二次函数的图象上是否存在点M,使△PQM是以点P为直角顶点的等腰直角三角形?若存在,请求出运动时间t;若不存在,请说明理由;
(4)如图②,点N的坐标为(﹣ ,0),线段PQ的中点为H,连接NH,当点Q关于直线NH的对称点Q′恰好落在线段BC上时,请直接写出点Q′的坐标.
,0),线段PQ的中点为H,连接NH,当点Q关于直线NH的对称点Q′恰好落在线段BC上时,请直接写出点Q′的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=900,∠B=∠E=300.



(1)操作发现如图2,固定△ABC,使△DEC绕点C旋转。当点D恰好落在BC边上时,填空:线段DE与AC的位置关系是 ;
② 设△BDC的面积为S1,△AEC的面积为S2。则S1与S2的数量关系是 。
(2)猜想论证
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC,CE边上的高,请你证明小明的猜想。
(3)拓展探究
已知∠ABC=600,点D是其角平分线上一点,BD=CD=4,OE∥AB交BC于点E(如图4),若在射线BA上存在点F,使S△DCF =S△BDC,请直接写出相应的BF的长
相关试题

