【题目】有4张写着以下数字的卡片,请按要求抽出卡片,完成下列各题:
![]()
(1)从中取出2张卡片,使这2张卡片上数字之积最大,最大值是________.
(2)从中取出2张卡片,使这2张卡片上数字之差最小,最小值是________.
(3)从中取出4张卡片,将这4个数字进行加、减、乘、除或乘方等混合运算,使结果为24,请写出一种符合要求的运算式子________.(注:4个数字都必须用到且只能用一次.)
参考答案:
【答案】10 -12 ![]()
【解析】
(1)观察这四个数,要找乘积最大的就要找符号相同且绝对值最大的数,所以选-5和-2;
(2)根据题意可知卡片中的最大数与最小数之间的差值即为所求;
(3)从中取出4张卡片,用学过的运算方法,使结果为24,这就不唯一,用加减乘除只要答数是24即可,比如![]() =24.
=24.
解:(1)根据题意得:(-5)×(-2)=10,
故答案为:10;
(2)由题意可得,从中取出2张卡片,使这2张卡片上数字的差最小,最小值是:-5-7=-12,
故答案为:-12;
(3)(答案不唯一)如![]() =24.
=24.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为-20,点B表示的数为16.动点P从点A出发,以每秒6个单位长度的速度沿数轴向右匀速运动,动点Q从点B出发,以每秒4个单位长度的速度沿数轴向左匀速运动.若点P、Q同时出发,设运动时间为t(t>0)秒.
(1)填空:①点A、B之间的距离为 ;
②点P表示的数为 ,点Q表示的数为 (用含t的代数式表示);
(2)当点P、Q到原点O的距离相等时,求t的值并求出此时点Q表示的数;
(3)若点P从点A出发到达点B后立刻返回到点A并保持速度不变,点Q到达点A时停止运动,问点P运动多少秒时与点Q相距6个单位长度?


-
科目: 来源: 题型:
查看答案和解析>>【题目】设一列数
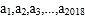 中任意三个相邻的数之和都是22,已知
中任意三个相邻的数之和都是22,已知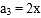 ,
,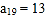 ,
,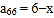 ,那么
,那么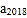 =________.
=________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AD平分∠BAC,DE⊥AB于E点,DF⊥AC于F点,有下列结论:①BD=DC;②DE=DF;③AD上任意一点到AB,AC的距离相等;④AD上任意一点到B点与C点的距离不等.其中正确的是( )

A. ①② B. ③④ C. ①②③ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知O为正方形ABCD的中心,M为射线OD上一动点(M与点O,D不重合),以线段AM为一边作正方形AMEF,连接FD.
(1)当点M在线段OD上时(如图1),线段BM与DF有怎样的数量及位置关系?请说明理由;
(2)当点M在线段OD的延长线上时(如图2),(1)中的结论是否仍然成立?请结合图2说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A=x-2y,B=-x-4y+1.
(1)求2(A+B)-(A-B);(结果用含x,y的代数式表示)
(2)当
 与
与 互为相反数时,求(1)中代数式的值.
互为相反数时,求(1)中代数式的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】火车站、机场、邮局等场所都有为旅客提供打包服务的项目.现有一个长、宽、高分别为a、b 、30的箱子(其中a>b),准备采用如图①、②的两种打包方式,所用打包带的总长(不计接头处的长)分别记为
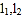 .
. 
(1)图①中打包带的总长
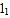 =________.
=________. 图②中打包带的总长
 =________.
=________.(2)试判断哪一种打包方式更节省材料,并说明理由.(提醒:先判断再说理,说理过程即为比较
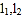 的大小.)
的大小.) (3)若b=40且a为正整数,在数轴上表示数
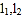 的两点之间有且只有19个整数点,求a 的值.
的两点之间有且只有19个整数点,求a 的值.
相关试题

