【题目】一次函数y=kx+4的图象经过点(-3,-2).
(1)求这个函数的解析式;
(2)画出该函数的图象;
(3)判断点(3,5)是否在此函数的图象上.
参考答案:
【答案】(1) y=2x+4;(2)如图所示见解析;(3)点(3,5)不在此函数的图象上.
【解析】整体分析:
(1)把(-3,-2)代入y=kx+4,即可求k值;(2)确定直线与x轴,y轴的交点后画函数图象;(3)把x=3代入到一次函数的解析式中,看函数值是否为5.
解:(1)把(-3,-2)代入y=kx+4,
得-3k+4=-2,解得k=2,
所以一次函数的解析式为y=2x+4.
(2)如图所示:
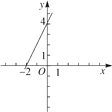
(3)当x=3时,y=2x+4=6+4=10≠5,
所以点(3,5)不在此函数的图象上.
-
科目: 来源: 题型:
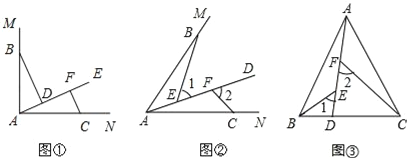
查看答案和解析>>【题目】(1)如图1,∠MAN=90°,射线AE在这个角的内部,点B、C分别在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.求证:△ABD≌△CAF;
(2)如图2,点B、C分别在∠MAN的边AM、AN上,点E、F都在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,且∠1=∠2=∠BAC.求证:△ABE≌△CAF;
(3)如图3,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,求△ACF与△BDE的面积之和.
-
科目: 来源: 题型:
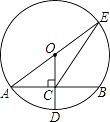
查看答案和解析>>【题目】如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )
A.2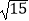
B.8
C.2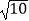
D.2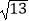
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一点,将Rt△ABC沿CD折叠,使B点落在AC边上的B′处,则∠CDB′等于( )

A.40°
B.60°
C.70°
D.80° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD,点F为正方形ABCD内一点,△BFC逆时针旋转后能与△BEA重合.
(1)旋转中心是点 ,旋转角度为 度;
(2)判断△BEF的形状为 ;
(3)若∠BFC=90°,说明AE∥BF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若m2-2mn+2n2-8n+16=0,求m、n的值.
解:∵m2-2mn+2n2-8n+16=0,
∴(m2-2m n+n2)+( )=0,
即( )2+( )2=0.根据非负数的性质,
∴m=n=
完善上述解答过程,然后解答下面的问题:
设等腰三角形ABC的三边长a、b、c,且满足a2+b2-4a-6b+13=0,求△ABC的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数的图象经过点A(2,1),B(﹣1,﹣3).
(1)求此一次函数的解析式;
(2)求此一次函数的图象与x轴、y轴的交点坐标;
(3)求此一次函数的图象与两坐标轴所围成的三角形面积.
相关试题

