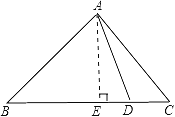
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,D是BC上的点.求证:BD2+CD2=2AD2.
参考答案:
【答案】证明过程见解析
【解析】
试题分析:作AE⊥BC于E,由于∠BAC=90°,AB=AC,所以BE=CE,要证明BD2+CD2=2AD2,只需找出BD、CD、AD三者之间的关系即可,由勾股定理可得出AD2=AE2+ED2,AE2=AB2﹣BE2=AC2﹣CE2,ED=BD﹣BE=CE﹣CD,代入求出三者之间的关系即可得证.
试题解析:作AE⊥BC于E,如上图所示: 由题意得![]() :ED=BD﹣BE=CE﹣CD,
:ED=BD﹣BE=CE﹣CD,
∵在△ABC中,∠BAC=90°,AB=AC, ∴BE=CE=BC, 由勾股定理可得:
AB2+AC2=BC2, AE2=AB2﹣BE2=AC2﹣CE2, AD2=AE2+ED2,
∴2AD2=2AE2+2ED2=AB2﹣BE2+(BD﹣BE)2+AC2﹣CE2+(CE﹣CD)2
=AB2+AC2+BD2+CD2﹣2BD×BE﹣2CD×CE =AB2+AC2+BD2+CD2﹣2×![]() BC×BC
BC×BC
=BD2+CD2, 即:BD2+CD2=2AD2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:mn2﹣4m= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】将0.000 015用科学记数法表示为( )
A. 1.5×10﹣5 B. 1.5×10﹣4 C. 1.5×10﹣3 D. 1.5×10﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】)多项式3x|m|y2+(m+2)x2y﹣1是四次三项式,则m的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将线段AB绕点A逆时针旋转60°得AC,连接BC,作△ABC的外接圆⊙O,点P为劣弧
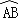 上的一个动点,弦AB、CP相交于点D.
上的一个动点,弦AB、CP相交于点D.(1)求∠APB的大小;
(2)当点P运动到何处时,PD⊥AB?并求此时CD:CP的值;
(3)在点P运动过程中,比较PC与AP+PB的大小关系,并对结论给予证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在同心圆中,大圆的弦AB交小圆于C、D两点.
(1)求证:∠AOC=∠BOD;
(2)试确定AC与BD两线段之间的大小关系,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】附加题:已知x、y互为相反数,a、b互为倒数,m的绝对值为3.求代数式4(x+y)﹣ab+m3的值.
相关试题

