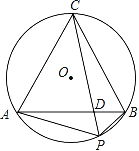
【题目】如图,将线段AB绕点A逆时针旋转60°得AC,连接BC,作△ABC的外接圆⊙O,点P为劣弧![]() 上的一个动点,弦AB、CP相交于点D.
上的一个动点,弦AB、CP相交于点D.
(1)求∠APB的大小;
(2)当点P运动到何处时,PD⊥AB?并求此时CD:CP的值;
(3)在点P运动过程中,比较PC与AP+PB的大小关系,并对结论给予证明.
参考答案:
【答案】(1)、120°;(2)、3:4;(3)、PC=AP+PB;证明过程见解析
【解析】
试题分析:(1)、先根据题意判断出△ABC是等边三角形,再根据圆内接四边形对角互补的性质可知∠APB+∠ACB=180°,进而可得出结论;(2)、连接PC,OA,OB,设⊙O的半径为r,则CP=2r,根据⊙O为等边△ABC的外接圆可求出∠OAB=30°,再根据直角三角形的性质可用r表示出OD,CD的值,进而得出结论;
(3)、在AP的延长线上取点Q,使PQ=PB,连接BQ,可判断出△BPQ是等边三角形,再根据全等三角形的判定定理得出△ABQ≌△CBP,由全等三角形的性质即可得出结论.
试题解析:(1)、∵AB=AC,∠BAC=60°, ∴△ABC是等边三角形,∵∠APB+∠ACB=180°,∴∠APB=120°
(2)、当点P运动到![]() 的中点时,PD⊥AB, 如图1,连接PC,OA,OB,设⊙O的半径为r,则CP=2r,
的中点时,PD⊥AB, 如图1,连接PC,OA,OB,设⊙O的半径为r,则CP=2r,
又∵⊙O为等边△ABC的外接圆, ∴∠OAB=30°, 在Rt△OAD中, ∵OD=![]() OA=
OA=![]() ,
,
∴CD=![]() +r=
+r=![]() , ∴CD:CP=
, ∴CD:CP=![]() :2r=3:4;
:2r=3:4;
(3)、PC=AP+PB

方法一: 如图2,在AP的延长线上取点Q,使PQ=PB,连接BQ, ∵∠APB=120°,
∴∠BPQ=60°, ∴△BPQ是等边三角形, ∴PB=BQ, ∵∠CBP=∠CBA+∠ABP=60°+∠ABP,
∠ABQ=∠QBP+∠ABP=60°+∠ABP, ∴∠ABQ=∠CBP, 在△ABQ和△CBP中,PB=QB,∠CBP=∠ABQ,CB=AB, ∴△ABQ≌△CBP, ∴CP=AQ=AP+PQ=AP+PB,即PC=AP+PB;
方法二:如图3,B为圆心,BP为半径画圆交CP于点M,连接BM, ∵∠CPB=60°,
∴△PBM是等边三角形, ∵∠CMB=120°, ∴∠CMB=∠APB, ∴△APB≌△CMB, ∴PC=AP+PB;
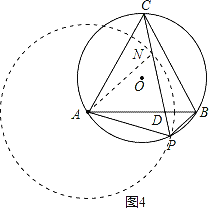
方法三:(略证)如图4,以A为圆心,A为半径画圆交CP于N,连接AN,
先证△APN是等边三角形,再证△ANC≌△APB, 从而PC=AP+PB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将0.000 015用科学记数法表示为( )
A. 1.5×10﹣5 B. 1.5×10﹣4 C. 1.5×10﹣3 D. 1.5×10﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】)多项式3x|m|y2+(m+2)x2y﹣1是四次三项式,则m的值为 .
-
科目: 来源: 题型:
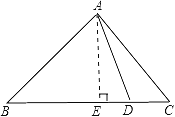
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AB=AC,D是BC上的点.求证:BD2+CD2=2AD2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在同心圆中,大圆的弦AB交小圆于C、D两点.
(1)求证:∠AOC=∠BOD;
(2)试确定AC与BD两线段之间的大小关系,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】附加题:已知x、y互为相反数,a、b互为倒数,m的绝对值为3.求代数式4(x+y)﹣ab+m3的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个点从数轴上的原点开始,先向左移动2cm到达A点,再向左移动3cm到达B点,然后向右移动9cm到达C点.
(1)用1个单位长度表示1cm,请你在数轴上表示出A、B、C三点的位置;
(2)把点C到点A的距离记为CA,则CA=cm.
(3)若点B以每秒2cm的速度向左移动,同时A、C点分别以每秒1cm、4cm的速度向右移动.设移动时间为t秒,试探索:CA﹣AB的值是否会随着t的变化而改变?请说明理由.
相关试题

