【题目】在平面直角坐标系中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1 , 作正方形A1B1C1C;延长C1B1交x轴于点A2 , 作正方形A2B2C2C1 , …按这样的规律进行下去,第2017个正方形的面积为 . 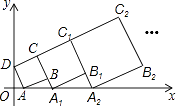
参考答案:
【答案】5×( ![]() )4032
)4032
【解析】解:设正方形的面积分别为S1,S2…,Sn,
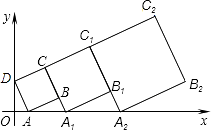
根据题意,得:AD∥BC∥C1A2∥C2B2,
∴∠BAA1=∠B1A1A2=∠B2A2x(同位角相等).
∵∠ABA1=∠A1B1A2=∠A2B2x=90°,
∴△BAA1∽△B1A1A2,
在直角△ADO中,根据勾股定理,得:AD= ![]() ,tan∠ADO=
,tan∠ADO= ![]() =
= ![]() ,
,
∵tan∠BAA1= ![]() =tan∠ADO,
=tan∠ADO,
∴BA1= ![]() AB=
AB= ![]() ,
,
∴CA1= ![]() +
+ ![]() ,
,
同理,得:C1A2=( ![]() +
+ ![]() )×(1+
)×(1+ ![]() ),
),
由正方形的面积公式,得:S1=( ![]() )2=5,
)2=5,
S2=( ![]() )2×(1+
)2×(1+ ![]() )2,
)2,
S3=( ![]() )2×(1+
)2×(1+ ![]() )4=5×(
)4=5×( ![]() )4,
)4,
由此,可得S2017=( ![]() )2×(1+
)2×(1+ ![]() )2×2016=5×(
)2×2016=5×( ![]() )4032.
)4032.
故答案为:5×( ![]() )4032.
)4032.
首先证明△AA1B∽△A1A2B1,从而可得到∠BAA1=∠B1A1A2,然后利用勾股定理计算出正方形的边长,最后利用正方形的面积公式计算第一个正方形的面积,从中找出规律,然后依据规律可求出第n个正方形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(习题回顾)(1)如下左图,在
 中,
中, 平分
平分 平分
平分 ,则
,则 _________
_________ .
.
(探究延伸)在
 中,
中, 平分
平分 、
、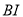 平分
平分 、
、 平分
平分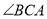 相交于点
相交于点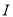 ,过点
,过点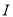 作
作 ,交
,交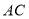 于点
于点 .
.(2)如上中间图,求证:
 ;
;(3)如上右图,
 外角
外角 的平分线
的平分线 与
与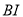 的延长线交于点
的延长线交于点 .
.①判断
 与
与 的位置关系,并说明理由;
的位置关系,并说明理由;②若
 ,试说明:
,试说明: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
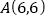 在直线
在直线 上,
上,(1)直线
 解析式为 ;
解析式为 ;(2)画出该一次函数的图象;
(3)将直线
 向上平移
向上平移 个单位长度得到直线
个单位长度得到直线 ,
, 与
与 轴的交点
轴的交点 的坐标为 ;
的坐标为 ;(4)直线
 与直线
与直线 相交于点
相交于点 ,
, 点坐标为 ;
点坐标为 ;(5)三角形ABC的面积为 ;
(6)由图象可知不等式
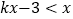 的解集为 .
的解集为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们在过去的学习中已经发现了如下的运算规律:
(1)15×15=1×2×100+25=225;
(2)25×25=2×3×100+25=625;
(3)35×35=3×4×100+25=1225;
……
按照这种规律,第n个式子可以表示为
A. n×n=
 ×(
×( +1)×100+25=n2
+1)×100+25=n2B. n×n=
 ×(
×( +1)×100+25=n2
+1)×100+25=n2C. (n+5)×(n+5)=n×(n+1)×100+25=n2+10n+25
D. (10n+5)×(10n+5)=n×(n+l)×l00+25=100n2+100n+25
-
科目: 来源: 题型:
查看答案和解析>>【题目】将九年级部分男生掷实心球的成绩进行整理,分成5个小组(x表示成绩,单位:米).A组:5.25≤x<6.25;B组:6.25≤x<7.25;C组:7.25≤x<8.25;D组:8.25≤x<9.25;E组:9.25≤x<10.25,并绘制出扇形统计图和频数分布直方图(不完整).规定x≥6.25为合格,x≥9.25为优秀.
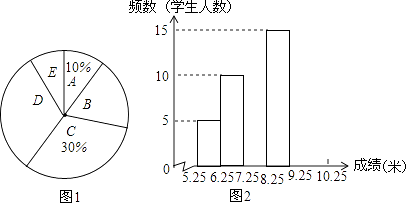
(1)这部分男生有多少人?其中成绩合格的有多少人?
(2)这部分男生成绩的中位数落在哪一组?扇形统计图中D组对应的圆心角是多少度?
(3)要从成绩优秀的学生中,随机选出2人介绍经验,已知甲、乙两位同学的成绩均为优秀,求他俩至少有1人被选中的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB=AD,BC=BD,若∠ABD=
 ∠BAC=,则∠BDC的度数为( )
∠BAC=,则∠BDC的度数为( )
A. 2B. 45°+
 C. 90°-D. 180°-3
C. 90°-D. 180°-3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处,某校数学课外兴趣小组的同学正在测量旗杆的高度,在旗杆的底部A处测得点D的仰角为15°,AC=10米,又测得∠BDA=45°.已知斜坡CD的坡度为i=1:
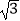 ,求旗杆AB的高度(
,求旗杆AB的高度(  ,结果精确到个位).
,结果精确到个位).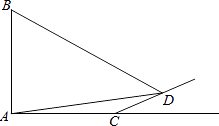
相关试题

