【题目】(习题回顾)(1)如下左图,在![]() 中,
中,![]() 平分
平分![]() 平分
平分![]() ,则
,则![]() _________
_________![]() .
.

(探究延伸)在![]() 中,
中,![]() 平分
平分![]() 、
、![]() 平分
平分![]() 、
、![]() 平分
平分![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() .
.
(2)如上中间图,求证:![]() ;
;
(3)如上右图,![]() 外角
外角![]() 的平分线
的平分线![]() 与
与![]() 的延长线交于点
的延长线交于点![]() .
.
①判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
②若![]() ,试说明:
,试说明:![]() .
.
参考答案:
【答案】(1)122;(2)证明见详解;(3)①![]() ,理由见解析;②理由见解析.
,理由见解析;②理由见解析.
【解析】
(1)根据三角形内角和为![]() 和角平分线的定义,可得
和角平分线的定义,可得![]() ,再利用三角形内角和,即可求得
,再利用三角形内角和,即可求得![]() 的大小;
的大小;
(2)根据根据三角形内角和为![]() 和角平分线的定义,可表达出
和角平分线的定义,可表达出![]() ,再用同样的方法表达出
,再用同样的方法表达出![]() ,即可证明;
,即可证明;
(3)①根据角平分线的定义,用等量代换的方法,分别表达出![]() 和
和![]() ,再根据内错角相等,两直线平行,即可得到结论;
,再根据内错角相等,两直线平行,即可得到结论;
②根据角平分线的定义,用等量代换的方法,分别表达出![]() 和
和![]() ,根据等腰三角形的要相等,即可得到结论.
,根据等腰三角形的要相等,即可得到结论.
(1)![]() 在
在![]() 中,
中,![]() 平分
平分![]() 平分
平分![]()
![]()
![]() .
.
(2)![]()
![]() 平分
平分![]() 、
、![]() 平分
平分![]() ,
,
![]() ,
,![]() ,
,
![]()
![]()
![]() 在
在![]() 中,
中,![]()
![]() ,
,
![]() 平分
平分![]() ,
,
![]() ,
,
![]()
![]() ,
,![]() ,
,
![]() ,
,
![]()
![]() .
.
(3)①![]() 与
与![]() 相平行,
相平行,
![]()
![]() 平分
平分![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]()
![]() .
.
②![]()
![]()
![]()
![]()
![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1=80°,∠2=100°,∠C=∠D.
(1)判断AC与DF的位置关系,并说明理由;
(2)若∠C比∠A大20°,求∠F的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是线段DE上一点,∠BAC=90°,AB=AC,BD⊥DE,CE⊥DE.
(1)求证:DE=BD+CE.
(2)如果是如图2这个图形,BD、CE、DE有什么数量关系?并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点
 的坐标为
的坐标为 ,点
,点 在第一象限且点
在第一象限且点 的纵坐标为
的纵坐标为 .当
.当 是腰长为
是腰长为 的等腰三角形时,则点
的等腰三角形时,则点 的坐标为_____.
的坐标为_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
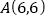 在直线
在直线 上,
上,(1)直线
 解析式为 ;
解析式为 ;(2)画出该一次函数的图象;
(3)将直线
 向上平移
向上平移 个单位长度得到直线
个单位长度得到直线 ,
, 与
与 轴的交点
轴的交点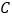 的坐标为 ;
的坐标为 ;(4)直线
 与直线
与直线 相交于点
相交于点 ,
, 点坐标为 ;
点坐标为 ;(5)三角形ABC的面积为 ;
(6)由图象可知不等式
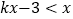 的解集为 .
的解集为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们在过去的学习中已经发现了如下的运算规律:
(1)15×15=1×2×100+25=225;
(2)25×25=2×3×100+25=625;
(3)35×35=3×4×100+25=1225;
……
按照这种规律,第n个式子可以表示为
A. n×n=
 ×(
×( +1)×100+25=n2
+1)×100+25=n2B. n×n=
 ×(
×( +1)×100+25=n2
+1)×100+25=n2C. (n+5)×(n+5)=n×(n+1)×100+25=n2+10n+25
D. (10n+5)×(10n+5)=n×(n+l)×l00+25=100n2+100n+25
-
科目: 来源: 题型:
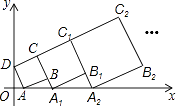
查看答案和解析>>【题目】在平面直角坐标系中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1 , 作正方形A1B1C1C;延长C1B1交x轴于点A2 , 作正方形A2B2C2C1 , …按这样的规律进行下去,第2017个正方形的面积为 .
相关试题

