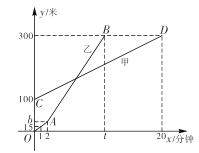
【题目】甲、乙二人都是户外运动爱好者,在一次登山活动中,甲、乙二人距出发点的高度![]() (单位:米),
(单位:米),![]() (单位:米)与乙登山时间 x (单位:分钟)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(单位:米)与乙登山时间 x (单位:分钟)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山的速度是每分钟 米,乙在 2 分钟时提速,提速时距地面的高度![]() 为______米;
为______米;
(2)若乙提速后,乙的速度是甲登山速度的 3 倍,请分别求出甲、乙二人登山全过程中,登山时距地面的高度![]() ,
, ![]() 与乙登山时间
与乙登山时间![]() 之间的函数关系式;
之间的函数关系式;
(3)在(2)的条件下,乙登山多长时间追上了甲? 此时乙距提速时的高度为多少米?
参考答案:
【答案】(1)10;30;(2)![]() ;
;![]() ;(3)6.5分钟;135米.
;(3)6.5分钟;135米.
【解析】
(1)根据函数图像由甲走的路程÷时间就可以算出甲的速度;根据函数图像可以求出乙在提速前每分离开地面的高度是15米,就可以求出b的值;
(2)乙提速后,乙的速度是甲登山速度的3倍,所以乙的速度是30米/分,那么就可以求出B点的坐标,加上A点的坐标代入一次函数解析式即可求出乙的解析式,把D、C坐标代入一次函数解析式求出甲的函数解析式;
(3)由(2)中的解析式联立方程求出其解就可以求出追上的时间,就可以求出乙离地面的高度,再减去A地的高度就可以得出结论.
(1)由函数图像得
甲的速度是:(300-100)÷20=10米/分;
在前2分钟内,设折线OA所在直线的解析式为:![]() ,其中
,其中![]() ,代入点(1,15),
,代入点(1,15),
解得![]() =15,故折线OA的解析式为:
=15,故折线OA的解析式为:![]() ,其中
,其中![]() ,
,
当x=2时代入,求得b=5×2=30米,
即乙在2分钟时提速,此时离地面的高度为30米.
故答案为:10;30
(2)∵乙提速时速度是甲的3倍,故乙提速后速度为:3×10=30米/分,
设AB所在直线的解析式为:![]() ,其中
,其中![]() ,
,
代入A(2,30),解得![]() ,
,
故AB所在直线解析式为:![]() ,
,
又由图知:当时间为t时,乙到达山顶,
故有:![]() ,解得
,解得![]() .
.
故折线AB的解析式为:![]() ,其中
,其中![]()
设CD的解析式为:![]() ,
,
将C(0,100),D(20,300)代入解析式中,求得![]() ,
,
![]() ,
,
故答案为:甲距离地面的高度与x的函数关系式为:![]()
乙距离地面的高度与x的函数关系式为:![]() ;
;
(3)图中AB和CD的交点处即表示乙追上甲,故联立方程组有:
![]() ,即:
,即:![]() ,解之得:
,解之得:![]()
即乙登山6.5分钟时乙追上了甲,此时乙距离提速时的高度为:6.5×10+100-30=135米.
故答案为:乙登山6.5分钟时追上了甲,此时乙距提速时的高度为135米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 在平面直角坐标系中,在正方形网格中,每个小正方形的边长为 1 个单位长度
在平面直角坐标系中,在正方形网格中,每个小正方形的边长为 1 个单位长度 (1)画出将
 向下平移 4 个单位长度后得到的
向下平移 4 个单位长度后得到的 ;
;(2)画出将
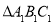 绕点 C 逆时针方向旋转
绕点 C 逆时针方向旋转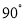 得到的
得到的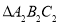 ;
;(3)在(2)的条件下,求线段
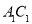 旋转到
旋转到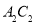 扫过的面积(结果保留
扫过的面积(结果保留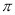 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
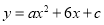 交
交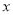 轴于
轴于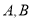 两点,交
两点,交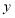 轴于点
轴于点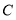 ,直线
,直线 经过点
经过点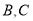 .
.(1)求抛物线的解析式;
(2)
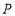 是直线
是直线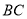 上方的抛物线上一动点,求
上方的抛物线上一动点,求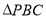 的最大面积.
的最大面积.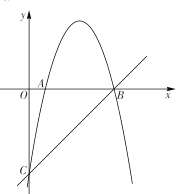
-
科目: 来源: 题型:
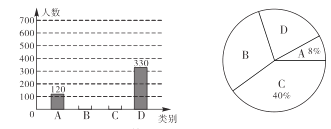
查看答案和解析>>【题目】近年来佳木斯市旅游事业发展迅速,“大亮子河森林公园”“富锦国家湿地公园”“赫哲民族文化村”“大来岗达勒花海”等景区愈来愈为人们所知晓 . 在一次调查中,根据市民对这四个景区的了解情况,按答题分数分为
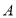 . 比较熟悉;
. 比较熟悉; 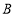 . 基本了解;
. 基本了解; 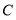 . 略有知晓;
. 略有知晓; 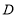 . 知之甚少,四类进行统计,绘制了以下两幅统计图(不完整),请根据图中信息解答以下各题:
. 知之甚少,四类进行统计,绘制了以下两幅统计图(不完整),请根据图中信息解答以下各题:(1)本次调查活动的样本容量是 ;
(2)补全条形统计图;
(3)“略有知晓”类占扇形统计图的圆心角是多少度? “知之甚少”类市民占被调查人数的百分比是多少?
(4)已知某小区有 5000 人,那么估计对这些景区“比较熟悉”的有多少人?
-
科目: 来源: 题型:
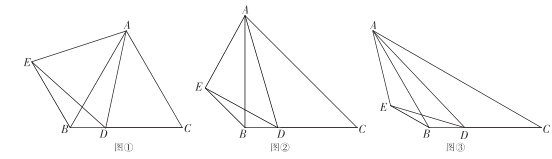
查看答案和解析>>【题目】如图,在△ABC中, AB=AC,D 为 BC 边上任意一点,以AD为底边向左侧作等腰△ADE,∠AED=∠ABC ,连接
 .
.(1)如图 ① ,当∠ABC=60°时,易证:CD=BE(不需要证明);
(2)当∠ABC=90°时,如图 ② ;当∠ABC=120°时,如图 ③ ;线段CD和BE又有怎样的关系? 并选择一个图形证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某电暖科技有限公司准备购进A型(直热式电暖)和B型(智能电风幕电暖)两种设备,经计算,购进 3 台A设备和 2 台B设备需用 6.6 万元,购进 1 台A设备和 3 台B设备需用5. 7 万元 .
请解答下列问题:
(1)求A、B两种设备的进价;
(2)该公司计划用 21 万元同时购进A、B两种设备,若A设备以每台1.5万元的价格出售,B设备以每台2万元的价格出售,且全部售出,请求出所获利润W(单位:万元)与购买A设备的资金m(单位:万元)之间的函数关系式;
(3)在(2)的条件下,要求A设备的利润不低于B设备的利润,并将(2)中的最大利润全部用于购买甲(小米笔记本4000元/台)、乙(华为笔记本6000元/台)两种型号的电脑赠给某中学,请求出有几种购买电脑的方案 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 在平面直角坐标系中,
在平面直角坐标系中, 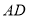 交
交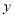 轴于点
轴于点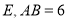 ,
,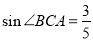 动点
动点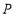 从原点出发,以每秒 1 个单位长度的速度沿
从原点出发,以每秒 1 个单位长度的速度沿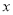 轴正方向移动,移动时间为
轴正方向移动,移动时间为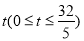 秒,过点 P 作垂直于
秒,过点 P 作垂直于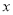 轴的直线
轴的直线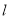 ,交
,交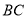 于点 M ,交
于点 M ,交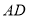 或
或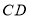 于点 N ,直线
于点 N ,直线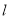 扫过矩形
扫过矩形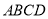 的面积为
的面积为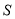 .
.(1)求点
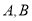 的坐标;
的坐标;(2)求直线
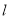 移动过程中到点
移动过程中到点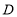 之前的
之前的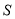 关于
关于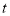 的函数关系式;
的函数关系式;(3)在直线
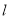 移动过程中,第一象限的直线
移动过程中,第一象限的直线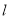 上是否存在一点
上是否存在一点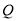 ,使
,使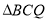 是等腰直角三角形? 若存在,直接写出点
是等腰直角三角形? 若存在,直接写出点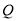 的坐标;若不存在,说明理由
的坐标;若不存在,说明理由
相关试题

