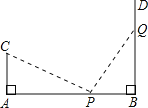
【题目】如图,AB=12米,CA⊥AB,垂足为点A,DB⊥AB,垂足为B,动点P从点B沿BA向点A方向移动,每分钟走1m,同时,点Q从点B沿BD向点D方向移动,每分钟走2m,已知CA=4m,几分钟后,△CAP≌PBQ?说明理由.
参考答案:
【答案】4分钟后,△CAP≌PBQ,理由见解析.
【解析】
设x分钟后,△CAP≌PBQ;由题意得出BP=x米,BQ=2x米,则AP=12-x(米),分两种情况:①当BP=AC=4时,x=4,由SAS得出△CAP≌PBQ;②当BP=AP时,x=12-x,解得:x=6,得出△CAP与PBQ不全等;即可得出结论.
4分钟后,△CAP≌PBQ,理由如下:
设x分钟后,△CAP≌PBQ;
根据题意得:BP=x米,BQ=2x米,则AP=12﹣x(米),
分两种情况:
①当BP=AC=4时,x=4,AP=12﹣4=8,BQ=8,
∴AP=BQ,
在△CAP和△PBQ中,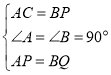
∴△CAP≌PBQ(SAS);
②当BP=AP时,x=12﹣x,
解得:x=6,
则BQ=12,AP=6,
∵AC=4,
∴AC≠BQ,
∴△CAP与PBQ不全等;
综上所述:4分钟后,△CAP≌PBQ.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
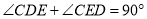 ,EM平分
,EM平分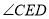 ,并与CD边交于点M.DN平分
,并与CD边交于点M.DN平分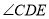 ,
,并与EM交于点N.
(1)依题意补全图形,并猜想
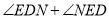 的度数等于 ;
的度数等于 ;(2)证明以上结论.
证明:∵ DN平分
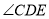 ,EM平分
,EM平分 ,
, ∴
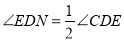 ,
,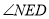 = .
= .(理由: )
∵
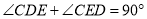 ,
,∴
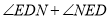 = ×(∠ +∠ )= ×90°= °.
= ×(∠ +∠ )= ×90°= °.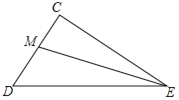
-
科目: 来源: 题型:
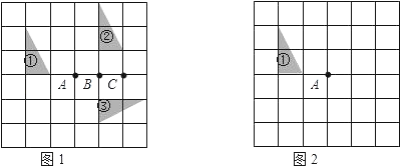
查看答案和解析>>【题目】在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,图①、图②、图③均为顶点都在格点上的三角形(每个小方格的顶点叫格点),
(1)在图1中,图①经过一次 变换(填“平移”或“旋转”或“轴对称”)可以得到图②;
(2)在图1中,图③是可以由图②经过一次旋转变换得到的,其旋转中心是点 (填“A”或 “B”或“C”);
(3)在图2中画出图①绕点A顺时针旋转90°后的图④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知n边形的内角和θ=(n-2)×180°.
(1)甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n.若不对,说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下,请补充完整.(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x
…
﹣3
﹣

﹣2
﹣1
0
1
2

3
…
y
…
3

m
﹣1
0
﹣1
0

3
…
其中,m= .
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出两条函数的性质.
(4)进一步探究函数图象发现:
①函数图象与x轴有 个交点,所以对应的方程x2﹣2|x|=0有 个实数根;
②方程x2﹣2|x|=2有 个实数根.

③关于x的方程x2﹣2|x|=a有4个实数根时,a的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠MON=60°,分别在OM、ON上截取OA=OB=3 cm,过B作BC⊥OM于C,再过B作射线BD⊥BC于B,连结AB.
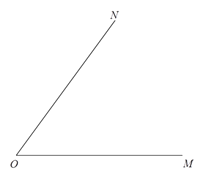
(1)画出图形;
(2)观察图形,写出直观估计∠ABC与∠MON的关系式;
(3)求∠NBD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】商场某种商品平均每天可销售30件,每件盈利50元。为了尽快减少库存,商场决定采取适当的降价措施。经调查发现,每件商品每降价1元,商场平均每天可多售出2件。设每件商品降价
 元。据此规律,请回答:
元。据此规律,请回答:(1)商场日销售量增加_____件,每件商品盈利_____元(用含
 的代数式表示)。
的代数式表示)。(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到2100元?
相关试题

