【题目】如图,∠MON=60°,分别在OM、ON上截取OA=OB=3 cm,过B作BC⊥OM于C,再过B作射线BD⊥BC于B,连结AB.
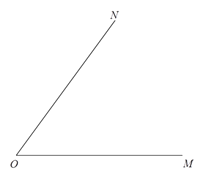
(1)画出图形;
(2)观察图形,写出直观估计∠ABC与∠MON的关系式;
(3)求∠NBD.
参考答案:
【答案】(1)详见解析;(2)2∠ABC=∠MON;(3)60°
【解析】
(1)根据题意即可作出图形;
(2)根据等边三角形的性质即可求解;
(3)根据平行线的性质即可求解.
解:(1)如图,所在图形如下:

(2)∵OA=OB,∠MON=60°,
∴△AOB是等边三角形,
∴∠BAO=60°,
∵BC⊥OM
∴∠ABC=90°-∠BAO=30°,
∴2∠ABC=∠MON;
(3)∵ BC⊥OM,BD⊥BC
∴BD∥OM
∴∠NBD=∠MON=60.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知n边形的内角和θ=(n-2)×180°.
(1)甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n.若不对,说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.
-
科目: 来源: 题型:
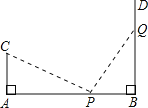
查看答案和解析>>【题目】如图,AB=12米,CA⊥AB,垂足为点A,DB⊥AB,垂足为B,动点P从点B沿BA向点A方向移动,每分钟走1m,同时,点Q从点B沿BD向点D方向移动,每分钟走2m,已知CA=4m,几分钟后,△CAP≌PBQ?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下,请补充完整.(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x
…
﹣3
﹣

﹣2
﹣1
0
1
2

3
…
y
…
3

m
﹣1
0
﹣1
0

3
…
其中,m= .
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出两条函数的性质.
(4)进一步探究函数图象发现:
①函数图象与x轴有 个交点,所以对应的方程x2﹣2|x|=0有 个实数根;
②方程x2﹣2|x|=2有 个实数根.

③关于x的方程x2﹣2|x|=a有4个实数根时,a的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】商场某种商品平均每天可销售30件,每件盈利50元。为了尽快减少库存,商场决定采取适当的降价措施。经调查发现,每件商品每降价1元,商场平均每天可多售出2件。设每件商品降价
 元。据此规律,请回答:
元。据此规律,请回答:(1)商场日销售量增加_____件,每件商品盈利_____元(用含
 的代数式表示)。
的代数式表示)。(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到2100元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2017四川省凉山州,第24题,8分)为了推进我州校园篮球运动的发展,2017年四川省中小学生男子篮球赛于2月在西昌成功举办.在此期间,某体育文化用品商店计划一次性购进篮球和排球共60个,其进价与售价间的关系如下表:

(1)商店用4200元购进这批篮球和排球,求购进篮球和排球各多少个?
(2)设商店所获利润为y(单位:元),购进篮球的个数为x(单位:个),请写出y与x之间的函数关系式(不要求写出x的取值范围);
(3)若要使商店的进货成本在4300元的限额内,且全部销售完后所获利润不低于1400元,请你列举出商店所有进货方案,并求出最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上A,B两点对应的有理数分别为10和15,点P从点A出发,以每秒1个单位长度的速度沿数轴正方向运动,点Q同时从原点O出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t秒.

(1)当0<t<5时,用含t的式子填空:
BP=_______,AQ=_______;
(2)当t=2时,求PQ的值;
(3)当PQ=
 AB时,求t的值.
AB时,求t的值.
相关试题

