【题目】甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x﹣4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.

(1)当a=﹣![]() 时,①求h的值;②通过计算判断此球能否过网.
时,①求h的值;②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为![]() m的Q处时,乙扣球成功,求a的值.
m的Q处时,乙扣球成功,求a的值.
参考答案:
【答案】(1)①![]() ,②能;(2)-
,②能;(2)-![]()
【解析】试题分析:(1)①将点P(0,1)代入![]() 即可求得h;②求出x=5时,y的值,与1.55比较即可得出判断;
即可求得h;②求出x=5时,y的值,与1.55比较即可得出判断;
(2)将(0,1)、(7, ![]() )代入
)代入![]() 代入即可求得a、h.
代入即可求得a、h.
(1)①当a=![]() 时,
时, ![]() ,将点P(0,1)代入,得:
,将点P(0,1)代入,得: ![]() ×16+h=1,解得:h=
×16+h=1,解得:h=![]() ;
;
②把x=5代入![]() ,得:
,得: ![]() =1.625,∵1.625>1.55,∴此球能过网;
=1.625,∵1.625>1.55,∴此球能过网;
(2)把(0,1)、(7, ![]() )代入
)代入![]() ,得:
,得: 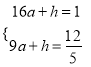 ,解得:
,解得: 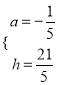 ,∴a=
,∴a=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在荔枝种植基地有A、B两个品种的树苗出售,已知A种比B种每株多20元,买1株A种树苗和2株B种树苗共需200元.
(1)问A、B两种树苗每株分别是多少元?
(2)为扩大种植,某农户准备购买A、B两种树苗共36株,且A种树苗数量不少于B种数量的一半,请求出费用最省的购买方案.
-
科目: 来源: 题型:
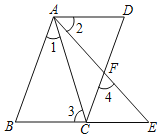
查看答案和解析>>【题目】如图,已知四边形ABCD,AB∥CD,点E是BC延长线上一点,连接AC、AE,AE交CD于点F,∠1=∠2,∠3=∠4.
证明:
(1)∠BAE=∠DAC;
(2)∠3=∠BAE;
(3)AD∥BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,点A,B的坐标分别是(-2,0),(4,0),现同时将点A、B分别向上平移2个单位长度,再向右平移2个单位长度,得到A,B的对应点C,D.连接AC、BD、CD.
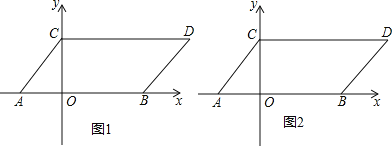
(1)点C的坐标为 ,点D的坐标为 ,四边形ABDC的面积为 .
(2)在x轴上是否存在一点E,使得△DEC的面积是△DEB面积的2倍?若存在,请求出点E的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4
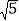 ,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )
,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )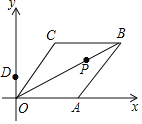
A. (0,0)B. (1,
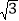 )C. (
)C. (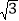 ,
,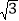 )D. (
)D. (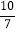 ,
, )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】一束光线从点A(3,3)出发,经过y轴上点C反射后经过点B(1,0),则光线从A点到B点经过的路线长是( )
A. 4B. 5C. 6D. 7
-
科目: 来源: 题型:
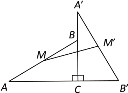
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,将△ABC绕点C顺时针旋转90°得到△A′B′C,M、M′分别是AB、A′B′的中点,若AC=8,BC=6,则线段MM′的长为____.
相关试题

