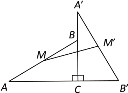
【题目】如图,在Rt△ABC中,∠C=90°,将△ABC绕点C顺时针旋转90°得到△A′B′C,M、M′分别是AB、A′B′的中点,若AC=8,BC=6,则线段MM′的长为____.
参考答案:
【答案】![]()
【解析】
先利用勾股定理求出AB的长,根据直角三角形斜边上的中线等于斜边的一半的性质求出CM=![]() AB,然后连接CM、CM′,再根据旋转的性质求出∠MCM′=90°,CM=CM′,再利用勾股定理列式求解即可.
AB,然后连接CM、CM′,再根据旋转的性质求出∠MCM′=90°,CM=CM′,再利用勾股定理列式求解即可.
连接CM,CM′,

∵AC=8,BC=6,
∴AB= ![]() =10,
=10,
∵M是AB的中点,
∴CM=![]() AB=5,
AB=5,
∵Rt△ABC绕点C顺时针旋转90°得到Rt△A′B′C,
∴∠A′CM′=∠ACM
∵∠ACM+∠MCB=90°,
∴∠MCB+∠BCM′=90°,
又∵CM=C′M′,
∴△CMM′是等腰直角三角形,
∴MM′=![]() CM=5
CM=5![]() ,
,
故答案为:5![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x﹣4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.

(1)当a=﹣
 时,①求h的值;②通过计算判断此球能否过网.
时,①求h的值;②通过计算判断此球能否过网.(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为
 m的Q处时,乙扣球成功,求a的值.
m的Q处时,乙扣球成功,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4
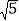 ,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )
,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )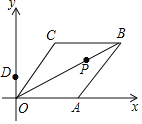
A. (0,0)B. (1,
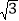 )C. (
)C. (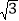 ,
,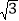 )D. (
)D. (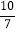 ,
, )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】一束光线从点A(3,3)出发,经过y轴上点C反射后经过点B(1,0),则光线从A点到B点经过的路线长是( )
A. 4B. 5C. 6D. 7
-
科目: 来源: 题型:
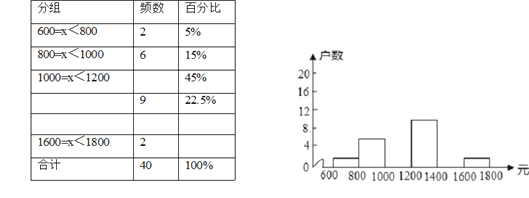
查看答案和解析>>【题目】小龙在学校组织的社会调查活动中负责了解他所居住的小区450户居民的家庭收入情况.他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.
根据以上提供的信息,解答下列问题:
(1)补全频数分布表.
(2)补全频数分布直方图.
(3)绘制相应的频数分布折线图.
(4)请你估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户?
-
科目: 来源: 题型:
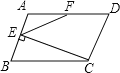
查看答案和解析>>【题目】如图在□ABCD中,BC=2AB,CE⊥AB于E,F为AD的中点,若∠AEF=52°,则∠B=___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解决问题.
学校要购买A,B两种型号的足球,按体育器材门市足球销售价格(单价)计算:若买2个A型足球和3个B型足球,则要花费370元,若买3个A型足球和1个B型足球,则要花费240元.
(1)求A,B两种型号足球的销售价格各是多少元/个?
(2)学校拟向该体育器材门市购买A,B两种型号的足球共20个,且费用不低于1300元,不超过1500元,则有哪几种购球方案?
相关试题

