【题目】如图1,在平面直角坐标系中,点A,B的坐标分别是(-2,0),(4,0),现同时将点A、B分别向上平移2个单位长度,再向右平移2个单位长度,得到A,B的对应点C,D.连接AC、BD、CD.
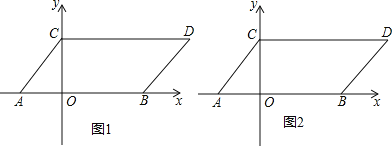
(1)点C的坐标为 ,点D的坐标为 ,四边形ABDC的面积为 .
(2)在x轴上是否存在一点E,使得△DEC的面积是△DEB面积的2倍?若存在,请求出点E的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)(0,2),(6,2),12;(2)点E的坐标为(1,0)和(7,0).
【解析】
(1)根据点平移的规律易得点C的坐标为(0,2),点D的坐标为(6,2);
(2)设点E的坐标为(x,0),根据△DEC的面积是△DEB面积的2倍和三角形面积公式得到![]() ×6×2=2×
×6×2=2×![]() ×|4-x|×2,解得x=1或x=7,然后写出点E的坐标.
×|4-x|×2,解得x=1或x=7,然后写出点E的坐标.
解:(1)∵点A,B的坐标分别是(-2,0),(4,0),现同时将点A、B分别向上平移2个单位长度,再向右平移2个单位长度得到A,B的对应点C,D,
∴点C的坐标为(0,2),点D的坐标为(6,2);
四边形ABDC的面积=2×(4+2)=12;
故答案为:(0,2),(6,2),12;
(2)存在.
设点E的坐标为(x,0),
∵△DEC的面积是△DEB面积的2倍,
∴![]() ×6×2=2×
×6×2=2×![]() ×|4-x|×2,解得x=1或x=7,
×|4-x|×2,解得x=1或x=7,
∴点E的坐标为(1,0)和(7,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=8,BC=6,点M从点D出发,以每秒2个单位长度的速度向点A运动,同时,点N从点B出发,以每秒1个单位长度的速度向点C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP⊥AD于点P,连接AC交NP于点Q,连接MQ.设运动时间为t秒.

(1)AM= ,AP= .(用含t的代数式表示)
(2)当四边形ANCP为平行四边形时,求t的值
(3)如图2,将△AQM沿AD翻折,得△AKM,是否存在某时刻t,
①使四边形AQMK为为菱形,若存在,求出t的值;若不存在,请说明理由
②使四边形AQMK为正方形,则AC= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在荔枝种植基地有A、B两个品种的树苗出售,已知A种比B种每株多20元,买1株A种树苗和2株B种树苗共需200元.
(1)问A、B两种树苗每株分别是多少元?
(2)为扩大种植,某农户准备购买A、B两种树苗共36株,且A种树苗数量不少于B种数量的一半,请求出费用最省的购买方案.
-
科目: 来源: 题型:
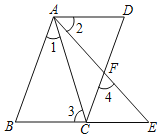
查看答案和解析>>【题目】如图,已知四边形ABCD,AB∥CD,点E是BC延长线上一点,连接AC、AE,AE交CD于点F,∠1=∠2,∠3=∠4.
证明:
(1)∠BAE=∠DAC;
(2)∠3=∠BAE;
(3)AD∥BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x﹣4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.

(1)当a=﹣
 时,①求h的值;②通过计算判断此球能否过网.
时,①求h的值;②通过计算判断此球能否过网.(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为
 m的Q处时,乙扣球成功,求a的值.
m的Q处时,乙扣球成功,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4
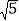 ,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )
,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )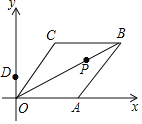
A. (0,0)B. (1,
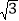 )C. (
)C. (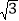 ,
,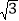 )D. (
)D. (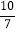 ,
, )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】一束光线从点A(3,3)出发,经过y轴上点C反射后经过点B(1,0),则光线从A点到B点经过的路线长是( )
A. 4B. 5C. 6D. 7
相关试题

