【题目】如图是作一个角的角平分线的方法:以![]() 的顶点
的顶点![]() 为圆心,以任意长为半径画弧,分别交
为圆心,以任意长为半径画弧,分别交![]() 于
于![]() 两点,再分别以
两点,再分别以![]() 为圆心,大于
为圆心,大于![]() 长为半径作画弧,两条弧交于点
长为半径作画弧,两条弧交于点![]() ,作射线
,作射线![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.

(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)若![]() ,垂足为
,垂足为![]() ,求证:
,求证:![]() .
.
参考答案:
【答案】(1)35°;(2)见解析.
【解析】
(1)首先根据OB∥FD,可得∠OFD+∠AOB=18O°,进而得到∠AOB的度数,再根据作图可知OP平分∠AOB,进而算出∠DOB的度数即可;
(2)首先证明∴∠AOD=∠ODF,再由FM⊥OD可得∠OMF=∠DMF,再加上公共边FM=FM,可利用AAS证明△FMO≌△FMD.
(1)解:∵OB∥FD,
∴∠OFD+∠AOB=18O°,
又∵∠OFD=110°,
∴∠AOB=180°∠OFD=180°110°=70°,
由作法知,OP是∠AOB的平分线,
∴∠DOB=![]() ∠ABO=
∠ABO=![]() ;
;
(2)证明:∵OP平分∠AOB,
∴∠AOD=∠DOB,
∵OB∥FD,
∴∠DOB=∠ODF,
∴∠AOD=∠ODF,
又∵FM⊥OD,
∴∠OMF=∠DMF,
在△MFO和△MFD中
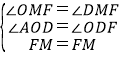
∴△MFO≌△MFD(AAS).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一枚质地均匀的正二十面体形状的骰子,其中的1个面标有“1”,2个面标有“2”, 3个面标有“3”,4个面标有“4”,5个面标有“5”,其余的面标有“6”.将这枚骰子掷出后:

(1)数字几朝上的概率最小?
(2)奇数面朝上的概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列给出的条件中,能判定四边形ABCD为平行四边形的是()
A.AB=BC,CD=DAB.AB//CD,AD=BC
C.AB//CD,∠A=∠CD.∠A=∠B,∠C=∠D
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售的一款空调机每台的标价是1635元,在一次促销活动中,按标价的八折销售,仍可盈利9%.
(1)求这款空调每台的进价(利润率=
 =
= ).
).(2)在这次促销活动中,商场销售了这款空调机100台,问盈利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分6分)我校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.

(1)这次被调查的同学共有 名;
(2)把条形统计图补充完整;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐.据此估算,该校1800名学生一餐浪费的食物可供多少人食用一餐?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,直线y=kx+1(k≠0)与双曲线y=
 (x>0)相交于P(1,m).
(x>0)相交于P(1,m).(1)求k的值;
(2)若点Q与点P关于y=x成轴对称,则点Q的坐标为Q( );
(3)若过P、Q两点的抛物线与y轴的交点为N(0,
 ),求该抛物线的解析式,并求出抛物线的对称轴方程.
),求该抛物线的解析式,并求出抛物线的对称轴方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,AB=12,BC=5,BE⊥DC交DC的延长线于点E.
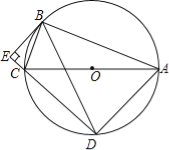
(1)求证:∠BCA=∠BAD;
(2)求DE的长;
(3)求证:BE是⊙O的切线.
相关试题

