【题目】如图,在平面直角坐标系中,△ABC和△A1B1C1关于点E成中心对称.

(1)画出对称中心E,并写出点E、A、C的坐标;
(2)P(a,b)是△ABC的边AC上一点,△ABC经平移后点P的对应点为P2(a+6,b+2),请画出上述平移后的△A2B2C2,并写出点A2、C2的坐标;
(3)判断△A2B2C2和△A1B1C1的位置关系(直接写出结果).
参考答案:
【答案】(1)作图见解析,E(-3,-1),A(-3,2),C(-2,0);(2)A2(3,4),C2(2,4);(3)△A2B2C2和△A1B1C1关于原点O成中心对称.
【解析】试题分析:(1)连接对应点,对应点的中点即为对称中心,在网格中可直接得出点E、A、C的坐标;
(2)根据“(a+6,b+2)”的规律求出对应点的坐标A2(3, 4),C2(4,2),顺次连接即可;
(3)由△A2B2C2和△A1B1C1的位置关系直接看出是关于原点O成中心对称.
试题解析:(1)如图,E(-3,-1),A(-3,2),C(-2,0);

(2)如图,A2(3,4),C2(2,4);
(3)△A2B2C2和△A1B1C1关于原点O成中心对称.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解今年初四学生的数学学习情况,某校在第一轮模拟测试后,对初四全体同学的数学成绩作了统计分析,绘制如下图表:请结合图表所给出的信息解答系列问题:
成绩
频数
频率
优秀
45
b
良好
a
0.3
合格
105
0.35
不合格
60
c

(1)该校初四学生共有多少人?
(2)求表中a,b,c的值,并补全条形统计图.
(3)初四(一)班数学老师准备从成绩优秀的甲、乙、丙、丁四名同学中任意抽取两名同学做学习经验介绍,求恰好选中甲、乙两位同学的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB=CD,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,若DE=BF,则下列结论:①CF=AE;②OE=OF;③四边形ABCD是平行四边形;④图中共有四对全等三角形.其中正确结论的个数是

A.4 B.3 C.2 D.1
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为15﹣20℃的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚里温度y(℃)随时间x(h)变化的函数图象,其中AB段是恒温阶段,BC段是双曲线y=
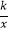 的一部分,请根据图中信息解答下列问题:
的一部分,请根据图中信息解答下列问题: 
(1)求k的值;
(2)恒温系统在一天内保持大棚里温度在15℃及15℃以上的时间有多少小时? -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)在平面直角坐标系中,
 OABC的边OC落在x轴的正半轴上,且点C(4,0),B(6,2),直线y=2x+b将
OABC的边OC落在x轴的正半轴上,且点C(4,0),B(6,2),直线y=2x+b将 OABC的面积平分,则b=_______.
OABC的面积平分,则b=_______.(2)在平面直角坐标系中,直线y=2x+3关于原点对称的直线的表达式为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=﹣
 x+6的图象与坐标轴交于A、B点(如图),AE平分∠BAO,交x轴于点E.
x+6的图象与坐标轴交于A、B点(如图),AE平分∠BAO,交x轴于点E.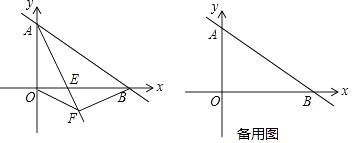
(1)求点B的坐标;
(2)求直线AE的表达式;
(3)过点B作BF⊥AE,垂足为F,连接OF,试判断△OFB的形状,并求△OFB的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5.OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.
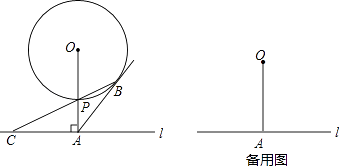
(1)试判断线段AB与AC的数量关系,并说明理由;
(2)若PC=2 ,求⊙O的半径和线段PB的长;
,求⊙O的半径和线段PB的长;
(3)若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,求⊙O的半径r的取值范围.
相关试题

