【题目】(10分)已知△ABC是等边三角形,点D是直线BC上一点,以AD为一边在AD的右侧作等边△ADE.
(1)如图①,点D在线段BC上移动时,直接写出∠BAD和∠CAE的大小关系;
(2)如图②,点D在线段BC的延长线上移动时,猜想∠DCE的大小是否发生变化.若不变请求出其大小;若变化,请说明理由.

参考答案:
【答案】(1)∠BAD=∠CAE;(2)∠DCE=60°,不发生变化.
【解析】试题分析:(1)由等边三角形的性质得出∠BAC=∠DAE,容易得出结论;
(2)由△ABC和△ADE是等边三角形可以得出AB=BC=AC,AD=AE,∠ABC=∠ACB=∠BAC=∠DAE=60°,得出∠ABD=120°,再证明△ABD≌△ACE,得出∠ABD=∠ACE=120°,即可得出结论;
解:(1)∠BAD=∠CAE;理由:
∵△ABC和△ADE是等边三角形,
∴∠BAC=∠DAE=60°,
∴∠BAD=∠CAE;
(2)∠DCE=60°,不发生变化;理由如下:
∵△ABC是等边三角形,△ADE是等边三角形,
∴∠DAE=∠BAC=∠ABC=∠ACB=60°,AB=AC,AD=AE.
∴∠ABD=120°,∠BAC﹣∠BAE=∠DAE﹣∠BAE
∴∠DAB=∠CAE.
在△ABD和△ACE中,
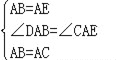 ,
,
∴△ABD≌△ACE(SAS),
∴∠ACE=∠ABD=120°.
∴∠DCE=∠ACE﹣∠ACB=120°﹣60°=60°.
点睛:本题考查了全等三角形的判定与性质以及等边三角形的性质;熟练掌握等边三角形的性质,证明三角形全等是解决问题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个城镇A、B与两条公路l1、l2位置如图所示,电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路l1,l2的距离也必须相等,那么点C应选在何处?请在图中,用尺规作图找出所有符合条件的点C.(不写已知、求作、作法,只保留作图痕迹)

-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形
 中,点
中,点 是对角线
是对角线 的中点,
的中点,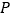 是对角线
是对角线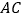 上一动点,过点
上一动点,过点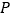 作
作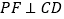 于点
于点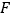 .如图
.如图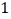 ,当点
,当点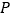 与点
与点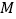 重合时,显然有
重合时,显然有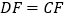 .
.(
 )如图
)如图 ,若点
,若点 在线段
在线段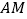 上(不与点
上(不与点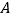 、
、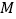 重合),
重合),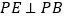 且
且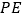 交
交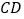 于点
于点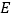 .
.求证:
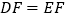 .
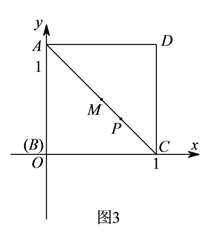
.(
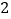 )如图所示建立直角坐标系,且正方形
)如图所示建立直角坐标系,且正方形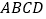 的边长为
的边长为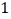 ,若点
,若点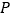 在线段
在线段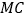 上(不与点
上(不与点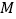 、
、 重合),
重合),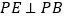 ,且
,且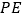 交直线
交直线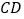 于点
于点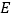 .请在图
.请在图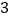 中作出示意图,并且求出当
中作出示意图,并且求出当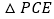 是一个等腰三角形时,
是一个等腰三角形时,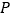 点的坐标为__________(直接写出答案).
点的坐标为__________(直接写出答案).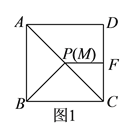

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形ABC中,∠B、∠C的平分线相交于点O,作BO、CO的垂直平分线分别交BC于点E、F.小明说:“E、F是BC的三等分点.”你同意他的说法吗?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示为一机器零件的三视图.
(1)请写出符合这个机器零件形状的几何体的名称.
(2)若俯视图中三角形为正三角形,那么请根据图中所标的尺寸,计算这个几何体的表面积(单位:cm2).

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点O到△ABC的两边AB、AC所在直线的距离OD=OE,且OB=OC.
(1)如图,若点O在BC上,求证:AB=AC;
(2)如图,若点O在△ABC的内部,求证:AB=AC;
(3)若点O在△ABC的外部,AB=AC成立吗?请画图表示.


-
科目: 来源: 题型:
查看答案和解析>>【题目】操作与探究.
(1)分别画出图①中“
 ”和“
”和“ ”关于直线l的对称图形(画出示意图即可).
”关于直线l的对称图形(画出示意图即可).(2)图②中小冬和小亮上衣上印的字母分别是什么?
(3)把字母“
 ”和“
”和“ ”写在薄纸上,观察纸的背面,写出你看到的字母背影.
”写在薄纸上,观察纸的背面,写出你看到的字母背影.(4)小明站在五个学生的身后,这五个学生正向前方某人用手势示意一个五位数,从小明站的地方看(如图③所示),这个五位数是23456.请你判断出他们示意的真实五位数是多少?

相关试题

