【题目】正方形![]() 中,点
中,点![]() 是对角线
是对角线![]() 的中点,
的中点,![]() 是对角线
是对角线![]() 上一动点,过点
上一动点,过点![]() 作
作![]() 于点
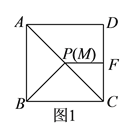
于点![]() .如图
.如图![]() ,当点
,当点![]() 与点
与点![]() 重合时,显然有
重合时,显然有![]() .
.
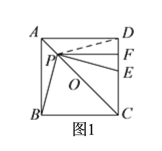
(![]() )如图
)如图![]() ,若点
,若点![]() 在线段
在线段![]() 上(不与点
上(不与点![]() 、
、![]() 重合),
重合),![]() 且
且![]() 交
交![]() 于点
于点![]() .
.
求证:![]() .
.
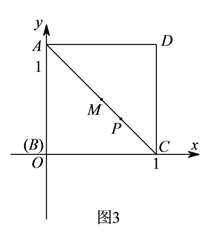
(![]() )如图所示建立直角坐标系,且正方形
)如图所示建立直角坐标系,且正方形![]() 的边长为
的边长为![]() ,若点
,若点![]() 在线段
在线段![]() 上(不与点
上(不与点![]() 、
、![]() 重合),
重合),![]() ,且
,且![]() 交直线
交直线![]() 于点
于点![]() .请在图
.请在图![]() 中作出示意图,并且求出当
中作出示意图,并且求出当![]() 是一个等腰三角形时,
是一个等腰三角形时,![]() 点的坐标为__________(直接写出答案).
点的坐标为__________(直接写出答案).

参考答案:
【答案】(![]() )见解析(
)见解析(![]() )
)![]()
【解析】试题分析:
(1)如图,连接PD,由正方形是关于对角线对称的轴对称图形和点P在AC上可得![]() ,
,![]() ;由
;由![]() ,
,![]() 可得
可得![]() ,结合
,结合![]() ,可得
,可得![]() ,从而可得
,从而可得![]() ,再结合
,再结合![]() 即可得到DF=EF;
即可得到DF=EF;
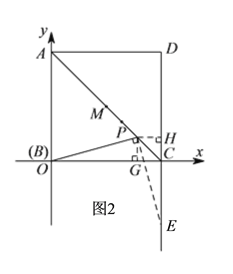
(2)如图2,先按要求画出图形,再过P作PG⊥x轴于点G,PH⊥y轴于点H,则由已知易得PG=PH=GC=HC,△BPG≌△EPH,从而可得EH=BG,设PG=a,则可得:GC=CH=a,PC=![]() ,BG=EH=1-a,CE=1-2a;由△PCE是等腰三角形和∠PCE是钝角可得:PC=CE,从而可得
,BG=EH=1-a,CE=1-2a;由△PCE是等腰三角形和∠PCE是钝角可得:PC=CE,从而可得![]() ,由此求得a的值即可得到点P的坐标了.
,由此求得a的值即可得到点P的坐标了.
试题解析:
(![]() )如图,连接
)如图,连接![]() ,
,
∵ 四边形![]() 是正方形,点P在对角线AC上,
是正方形,点P在对角线AC上,
∴ 由正方形关于对角线AC对称可得:![]() ,
,![]() ,
,
∵ ![]() ,
,![]() ,
,
∴ ![]() ,
,
∵ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∵ ![]() ,
,
∵ ![]() .
.
(![]() )
)![]() 点坐标为
点坐标为![]() ,
,
过点![]() 作
作![]() 轴,
轴,![]() 轴,
轴,
∵ 四边形![]() 是正方形,
是正方形,![]() 为对角线,
为对角线,
∴ ![]() ,
,![]() ,
,
又∵![]() ,
,
∴ ![]() ,
,
∴ ![]() ≌
≌![]() ,
,
∴ ![]() ,
,
设![]() ,则
,则![]() ,PC=
,PC=![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∵ ![]() 为钝角,
为钝角,
∴ 当![]() 为等腰三角形时,
为等腰三角形时, ![]() ,
,
∵ ![]() ,
,![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() 点坐标为
点坐标为![]() .
.
-
科目: 来源: 题型:
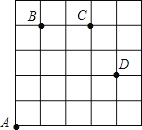
查看答案和解析>>【题目】如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(﹣1,﹣4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中
(1)A→C( , ),B→D( , );
(2)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程;
(3)若这只甲虫从A处去甲虫P处的行走路线依次为(+2,+2),(+1,﹣1),(﹣2,+3),(﹣1,﹣2),请在图中标出依次行走停点E、F、M、N的位置.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=30°,OP平分∠AOB,PD⊥OB于D,PC∥OB交OA于C,若PC=6,则PD= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】两个城镇A、B与两条公路l1、l2位置如图所示,电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路l1,l2的距离也必须相等,那么点C应选在何处?请在图中,用尺规作图找出所有符合条件的点C.(不写已知、求作、作法,只保留作图痕迹)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形ABC中,∠B、∠C的平分线相交于点O,作BO、CO的垂直平分线分别交BC于点E、F.小明说:“E、F是BC的三等分点.”你同意他的说法吗?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)已知△ABC是等边三角形,点D是直线BC上一点,以AD为一边在AD的右侧作等边△ADE.
(1)如图①,点D在线段BC上移动时,直接写出∠BAD和∠CAE的大小关系;
(2)如图②,点D在线段BC的延长线上移动时,猜想∠DCE的大小是否发生变化.若不变请求出其大小;若变化,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示为一机器零件的三视图.
(1)请写出符合这个机器零件形状的几何体的名称.
(2)若俯视图中三角形为正三角形,那么请根据图中所标的尺寸,计算这个几何体的表面积(单位:cm2).

相关试题

