【题目】
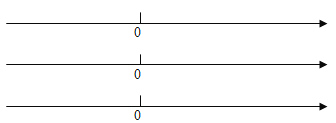
(1)点A表示的数为 ,点B表示的数为 ,点C表示的数为 .
(2)用含t的代数式表示P到点A和点C的距离: PA= ,PC= .
(3)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回,运动到终点A.①在点Q向点C运动过程中,能否追上点P?若能,请求出点Q运动几秒追上.②在点Q开始运动后,P、Q两点之间的距离能否为2个单位?如果能,请求出此时点P表示的数;如果不能,请说明理由.
参考答案:
【答案】(1)A:—26 B:-10 C:10
(2)PA=![]()
![]()
(3)①8
②![]() 对应的p点分别为
对应的p点分别为![]()
【解析】试题(1)根据:数轴上点A与点B的距离为16个单位长度,点A在原点的左侧,到原点的距离为26个单位长度,点B在点A的右侧,点C表示的数与点B表示的数互为相反数,可以确定A、B、C点对应的数;(2)因为动点P从A出发,以每秒1个单位的速度向终点C移动,且移动时间为t秒,所以PA=![]()
![]() ;(3)①设运动时间是t秒,根据点Q追上点P时,点Q运动的路程=点P运动的路程,列出关于t的方程,求出方程的解即可得到结果.②分情况讨论:点Q从A点向点C运动时,又分点Q在点P的后面与点Q在点P的前面;点Q从C点返回到点A时,又分点Q在点P的后面与点Q在点P的前面.
;(3)①设运动时间是t秒,根据点Q追上点P时,点Q运动的路程=点P运动的路程,列出关于t的方程,求出方程的解即可得到结果.②分情况讨论:点Q从A点向点C运动时,又分点Q在点P的后面与点Q在点P的前面;点Q从C点返回到点A时,又分点Q在点P的后面与点Q在点P的前面.
试题解析: 解:(1)根据题意可得:点A表示的数为-26,点B表示的数为-10,点C表示的数为10;(2)因为动点P从A出发,以每秒1个单位的速度向终点C移动,且移动时间为t秒,所以PA=![]() ,
,![]() ;(3)①设运动时间是t秒,根据点Q追上点P时,点Q运动的路程=点P运动的路程,列方程得:3t=1×(t+16),解得t=8;②分两种情况:(Ⅰ)点Q从A点向点C运动时,如果点Q在点P的后面,那么1×(t+16)-3t=2,解得t=7,此时点P表示的数是-3;如果点Q在点P的前面,那么3t-1×(t+16)=2,解得t=9,此时点P表示的数是-1;(Ⅱ)点Q从C点返回到点A时,如果点Q在点P的后面,那么3t+1×(t +16)+2=2×36,解得t=
;(3)①设运动时间是t秒,根据点Q追上点P时,点Q运动的路程=点P运动的路程,列方程得:3t=1×(t+16),解得t=8;②分两种情况:(Ⅰ)点Q从A点向点C运动时,如果点Q在点P的后面,那么1×(t+16)-3t=2,解得t=7,此时点P表示的数是-3;如果点Q在点P的前面,那么3t-1×(t+16)=2,解得t=9,此时点P表示的数是-1;(Ⅱ)点Q从C点返回到点A时,如果点Q在点P的后面,那么3t+1×(t +16)+2=2×36,解得t=![]() ,此时点P表示的数是
,此时点P表示的数是![]() ;如果点Q在点P的前面,那么3 t +1×(t +16)=2×36+2,解得t =
;如果点Q在点P的前面,那么3 t +1×(t +16)=2×36+2,解得t =![]() ,此时点P表示的数是
,此时点P表示的数是![]() .
.
答:在点Q开始运动后,P、Q两点之间的距离能为2个单位,此时点P表示的数分别![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰三角形ABC中,∠ABC=90°,D为AC边上中点,过D点作DE⊥DF,交AB于E,交BC于F,若S四边形BFDE=9,则AB的长为:
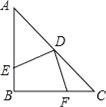
A. 3 B. 6 C. 9 D. 18
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC与BD相交于点O,∠D=∠C,添加下列哪个条件后,仍不能使△ADO≌△BCO的是( )

A. AD=BC B. AC=BD C. OD=OC D. ∠ABD=∠BAC
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据如下解方程
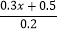 =
=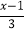 的过程,仿照实例在每个步骤前面的括号内填写该步骤的名称,后面的括号内填写这样变形的依据,在最后的横线上写出方程的解.
的过程,仿照实例在每个步骤前面的括号内填写该步骤的名称,后面的括号内填写这样变形的依据,在最后的横线上写出方程的解.解:原方程可变形为
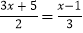 .(分数的基本性质)
.(分数的基本性质)去分母,得3(3x+5)=2(x–1).(__________)
去括号,得9x+15=2x–2.(__________)
(__________),得9x–2x=–15–2.(__________)
合并同类项,得7x=–17.
(__________),得x=__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB⊥BC,AD⊥DC,∠BAD=100°,在BC、CD上分别找一点M、N,当△AMN的周长最小时,∠AMN+∠ANM的度数是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OA⊥OC,OB⊥OD,①∠AOB=∠COD;②∠BOC+∠AOD=180°;③∠AOB+∠COD=90°;④图中小于平角的角有6个;其中正确的结论有几个( )
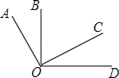
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
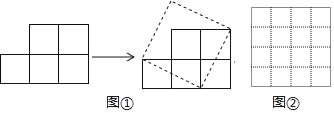
查看答案和解析>>【题目】如图①,将一个由五个边长为1的小正方形组成的图形剪开可以拼成一个正方形.
(1)拼成的正方形的面积与边长分别是多少?
(2)你能在图②中连结四个格点(每一个小正方形的顶点叫做格点),画出一个面积为10的正方形吗?如果不能,请说明理由;如果能,请在图②中画出这个正方形.
相关试题

