【题目】如图,在等腰三角形ABC中,∠ABC=90°,D为AC边上中点,过D点作DE⊥DF,交AB于E,交BC于F,若S四边形BFDE=9,则AB的长为:
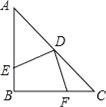
A. 3 B. 6 C. 9 D. 18
参考答案:
【答案】B
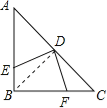
【解析】试题分析:首先连接BD,由已知等腰直角三角形ABC,可推出BD⊥AC且BD=CD=AD,∠ABD=45°再由DE丄DF,可推出∠FDC=∠EDB,又等腰直角三角形ABC可得∠C=45°,所以△EDB≌△FDC,所以四边形的面积是三角形ABC的一半,利用三角形的面积公式即可求出AB的长.
解:连接BD,
∵等腰直角三角形ABC中,D为AC边上中点,
∴BD⊥AC(三线合一),BD=CD=AD,∠ABD=45°,
∴∠C=45°,
∴∠ABD=∠C,
又∵DE丄DF,
∴∠FDC+∠BDF=∠EDB+∠BDF,
∴∠FDC=∠EDB,
在△EDB与△FDC中,
∵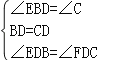 ,
,
∴△EDB≌△FDC(ASA),
∴S四边形面积=S△BDC=![]() S△ABC=9,
S△ABC=9,
∴![]() AB2=18,
AB2=18,
∴AB=6,
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.x6÷x2=x3B.(2a3)2=4a5
C.x2+x4=x6D.(﹣2a)2a=4a3
-
科目: 来源: 题型:
查看答案和解析>>【题目】【问题情境】
课外兴趣小组活动时,老师提出了如下问题:
如图①,△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使DE=AD,连接BE.请根据小明的方法思考:
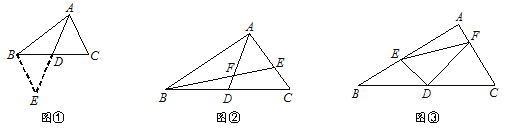
(1)由已知和作图能得到△ADC≌△EDB,依据是 .
A.SSS B.SAS C.AAS D.HL
(2)由“三角形的三边关系”可求得AD的取值范围是 .
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
【初步运用】
如图②,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.若EF=3,EC=2,求线段BF的长.
【灵活运用】
如图③,在△ABC中, ∠A=90°,D为BC中点, DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.试猜想线段BE、CF、EF三者之间的等量关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若∠α补角是∠α余角的3倍,则∠α= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某城市计划用两年时间增加全市绿化面积,若平均每年绿化面积比上一年增长20%,则两年后城市绿化面积是原来的( )
A.1.2倍B.1.4倍C.1.44倍D.1.8倍
-
科目: 来源: 题型:
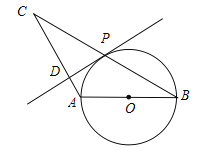
查看答案和解析>>【题目】已知:如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点P,PD⊥AC于点D.
(1)、求证:PD是⊙O的切线;(6分)(2)、若∠CAB=120°,AB=2,求BC的值.(6分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a<b,则下列不等式不成立的是( )
A. 3a<3b B. ﹣3a<﹣3b C. a+3<b+3 D. 2a﹣1<2b﹣1
相关试题

