【题目】如图,已知四边形ABCD是平行四边形,BC=3AB,A,B两点的坐标分别是(﹣1,0),(0,2),C,D两点在反比例函数y= ![]() (x<0)的图象上,则k的值等于 .
(x<0)的图象上,则k的值等于 . 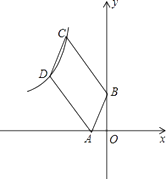
参考答案:
【答案】-24
【解析】解:设点C坐标为(a, ![]() ),(a<0),点D的坐标为(x,y).
),(a<0),点D的坐标为(x,y).
∵四边形ABCD是平行四边形,
∴AC与BD的中点坐标相同,
∴(a﹣1, ![]() +0)=(x+0,y+2),
+0)=(x+0,y+2),
则x=a﹣1,y= ![]() ,
,
代入y= ![]() ,可得:k=2a﹣2a2 ①;
,可得:k=2a﹣2a2 ①;
在Rt△AOB中,AB= ![]() =
= ![]() ,
,
∴BC=3AB=3 ![]() ,
,
故BC2=(0﹣a)2+( ![]() ﹣2)2=(3
﹣2)2=(3 ![]() )2 ,
)2 ,
整理得:a4+k2﹣4ka=41a2 ,
将①k=2a﹣2a2 , 代入后化简可得:a2=9,
∵a<0,
∴a=﹣3,
∴k=﹣6﹣18=﹣24.
所以答案是:﹣24.
方法二:
因为ABCD是平行四边形,所以点C、D是点A、B分别向左平移a,向上平移b得到的.
故设点C坐标是(﹣a,2+b),点D坐标是(﹣1﹣a,b),(a>0,b>0)
根据K的几何意义,|﹣a|×|2+b|=|﹣1﹣a|×|b|,
整理得2a+ab=b+ab,
解得b=2a.
过点D作x轴垂线,交x轴于H点,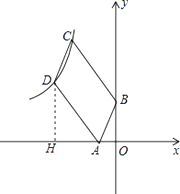
在直角三角形ADH中,
由已知易得AD=3 ![]() ,AH=a,DH=b=2a.
,AH=a,DH=b=2a.
AD2=AH2+DH2 , 即45=a2+4a2 ,
得a=3.
所以D坐标是(﹣4,6)
所以|k|=24,由函数图象在第二象限,
所以k=﹣24.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,垂足为D.
(1)求作∠ABC的平分线(要求:尺规作图,保留作图痕迹,不写作法);
(2)若∠ABC的平分线分别交AD,AC于P,Q两点,证明:AP=AQ.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:已知△ABC为直角三角形,分别以直角边AC、BC为直径作半圆AmC和BnC,以AB为直径作半圆ACB,记两个月牙形阴影部分的面积之和为S1,△ABC的面积为S2,则S1与S2的大小关系为( )

A. S1>S2 B. S1<S2 C. S1=S2 D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两建筑物的水平距离BC为18m,从A点测得D点的俯角α为30°,测得C点的俯角β为60°.则建筑物CD的高度为m(结果不作近似计算).

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:|
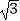 ﹣2|+20100﹣(﹣
﹣2|+20100﹣(﹣  )﹣1+3tan30°.
)﹣1+3tan30°. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学九(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题:
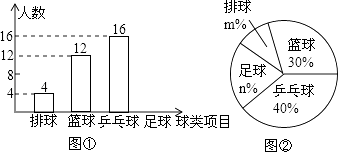
(1)九(1)班的学生人数为 , 并把条形统计图补充完整;
(2)扇形统计图中m= , n= , 表示“足球”的扇形的圆心角是度;
(3)排球兴趣小组4名学生中有3男1女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】自开展“学生每天锻炼1小时”活动后,我市某中学根据学校实际情况,决定开设A:毽子,B:篮球,C:跑步,D:跳绳四种运动项目.为了了解学生最喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如图统计图.请结合图中信息解答下列问题:
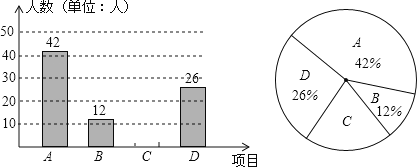
(1)该校本次调查中,共调查了多少名学生?
(2)请将两个统计图补充完整;
(3)在本次调查的学生中随机抽取1人,他喜欢“跑步”的概率有多大?
相关试题

