搜索
【题目】(1)化简:
(2)计算:
；
(3)化简:
；
(4)已知
求代数式
的值；
(5)已知
求代数式
的值.
参考答案：
【答案】（1）2xy-y2；（2）1；（3）-11a6；（4）6；（5）13.
【解析】
（1）原式第一项利用单项式乘以多项式的运算法则进行计算，第二项运用完全平方公式进行计算，去括号合并同类项即可得到结果；
（2）原式第二项2010变成2009+1，2008变成2009-1，利用平方差公式化简，去括号合并即可得到结果；
（3）原式先利用积的乘方和幂的乘方运算法则进行计算，合并同类项即可得到结果；
（4）先根据整式的混合运算顺序和运算法则进行化简，再将
即
整体代入即可；
（5）先根据多项式除以单项式的法则计算原式，再将n的值代入计算即可得结果.
（1）
=
=
；
（2）
=
=
=1；
（3）
=
=
；
（4）
=
=
当即时，
原式=3（
）+9
=-3+9
=6；
（5）
=2n2-2n+1
当n=-2时，
原式=
=8+4+1
=13.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，∠AOB=30°，OC为∠AOB内部一条射线，点P为射线OC上一点，OP=4，点M、N分别为OA、OB边上动点，则△MNP周长的最小值为（ ）
A.
B. 
C. 
D. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图是一个平均被分成6等分的圆，每一个扇形中都标有相应的数字，甲乙两人分别转动转盘，设甲转动转盘后指针所指区域内的数字为x，乙转动转盘后指针所指区域内的数字为y（当指针在边界上时，重转一次，直到指向一个区域为止）．
（1）直接写出甲转动转盘后所指区域内的数字为负数的概率；
（2）用树状图或列表法，求出点（x，y）落在第二象限内的概率．
-
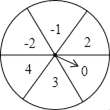
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A(－2，1)，B(－1，4)，C(－3，2)．
(1)画出△ABC关于点B成中心对称的图形△A1BC1；
(2)以原点O为位似中心，相似比为1∶2，在y轴的左侧，画出△ABC放大后的图形△A2B2C2，并直接写出点C2的坐标.
-
科目： 来源： 题型：
查看答案和解析>>【题目】（本小题满分8分）某商家预测一种应季衬衫能畅销市场，就用13200元购进了一批这种衬衫，面市后果然供不应求．商家又用28800元购进了第二批这种衬衫，所购数量是第一批购进量的2倍，但单价贵了10元．
（1）该商家购进的第一批衬衫是多少件？
（2）若两批衬衫按相同的标价销售，最后剩下50件按八折优惠卖出，如果两批衬衫全部售完后利润率不低于25%（不考虑其它因素），那么每件衬衫的标价至少是多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】填空，把下面的推理过程补充完整，并在括号内注明理由：
如图，已知A、B、C、D在同一直线上，AE∥DF，AC=BD，∠E=∠F，求证:BE∥CF.
证明:∵AE∥DF(已知)
∴_________(两直线平行，内错角相等)
∵AC=BD(已知)
又∵AC=AB+BC，BD=BC+CD
∴________(等式的性质)
∵∠E=∠F(已知）
∴△ABE≌△DCF(___________)
∴∠ABE=∠DCF(_________________)
∵ABF+∠CBE=180°，∠DCF+∠BCF=180°
∴∠CBE=∠BCF(__________________)
∴BE∥CF(________________________)
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面的材料并填空：
①(1﹣
)(1+)＝1﹣
，反过来，得1﹣＝(1﹣)(1+)＝×
；②(1﹣
)(1+)＝1﹣
，反过来，得1﹣＝(1﹣)(1+)＝ × ；③(1﹣
)(1+)＝1﹣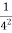
，反过来，得1﹣＝ ＝
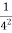；利用上面的材料中的方法和结论计算下题：
(1﹣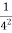
)(1﹣)(1﹣)……(1﹣
)(1﹣
)(1﹣
).
相关试题
