【题目】如图,已知四边形ABCD是梯形,AD∥BC,∠A=90°,BC=BD,CE⊥BD,垂足为E.
(1)求证:△ABD≌△ECB;
(2)若∠DBC=50°,求∠DCE的度数.

参考答案:
【答案】解: (1)证明:∵ AD∥BC,∴∠ADB=∠EBC。
∵ 在△ABD和△ECB中 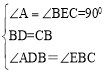 ,
,
∴△ABD≌△ECB(ASA)。--- -- 3分
(2)∵BC=BD,∠DBC=50°,∴∠BCD=65°。
又∵∠BEC=90°,∴∠BCE=40°。
∴∠DCE=∠BCD-∠BCE=65°-40°=25°。
【解析】(1)∵ AD∥BC,∴∠ADB=∠EBC,再加上BC=BD,∠A=90°,CE⊥BD,即可得△ABD≌△ECB;
由BC=BD根据等边对等角可求出∠BCD,再利用三角形内角和求出∠BCE,即可求到∠DCE。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中,不能运用平方差公式计算的是( )
A. (ab-1)(ab+1) B. (2x-1)(-1+2x)
C. (-2x-y)(2x-y) D. (-a+5)(-a-5)
-
科目: 来源: 题型:
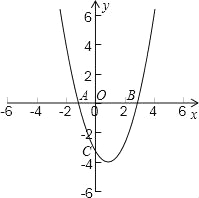
查看答案和解析>>【题目】在直角坐标平面中,O为坐标原点,二次函数y=x2+bx+c的图象与x轴的负半轴相交于点C(如图),点C的坐标为(0,﹣3),且BO=CO
(1)求这个二次函数的解析式;
(2)设这个二次函数的图象的顶点为M,求AM的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=(a-1)x2-x+a2-1的图象经过原点,则a的值为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上三点A,O,B对应的数分别为﹣3,0,1,点P为数轴上任意一点,其表示的数为x.
(1)如果点P到点A,点B的距离相等,那么x=;
(2)当x=时,点P到点A、点B的距离之和是6;
(3)若点P到点A,点B的距离之和最小,则x的取值范围是;
(4)在数轴上,点M,N表示的数分别为x1 , x2 , 我们把x1 , x2之差的绝对值叫做点M,N之间的距离,即MN=|x1﹣x2|.
若点P以每秒3个单位长度的速度从点O向左运动时,点E以每秒1个单位长度的速度从点A向左运动、点F以每秒4个单位长度的速度从点B也向左运动,且三个点同时出发,那么运动秒时,点P到点E,点F的距离相等. -
科目: 来源: 题型:
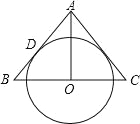
查看答案和解析>>【题目】如图,AO是△ABC的中线,⊙O与AB边相切于点D.
(1)要使⊙O与AC边也相切,应增加条件 (任写一个);
(2)增加条件后,请你说明⊙O与AC边相切的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从2016年1月1日开始,北京市居民生活用气阶梯价格制度将正式实施,一般生活用气收费标准如下表所示,比如6口以下的户年天然气用量在第二档时,其中350立方米按28元/m3收费,超过350立方米的部分按2.5元/m3收费.小冬一家有五口人,他想帮父母计算一下实行阶梯价后,家里天然气费的支出情况.
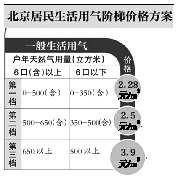
(1)如果他家2016年全年使用300立方米天然气,那么需要交多少元天然气费?
(2)如果他家2016年全年使用500立方米天然气,那么需要交多少元天然气费?
(3)如果他家2016年需要交1563元天然气费,他家2016年用了多少立方米天然气?
相关试题

