【题目】为了迎接体育中考,某校九年级开展了体育中考项目的第一次模拟测验. 下图为某校九年级同学各项目达标人数统计图: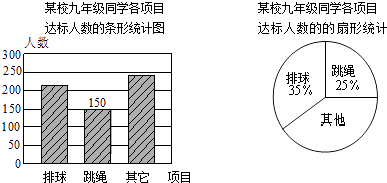
(1)在九年级学生中,达标的总人数是;
(2)在扇形统计图中,表示“其他”项目扇形的圆心角的度数是;
(3)经过一段时间的练习,在第二次模拟测验中,“排球”项目达标的人数增长到了231人,则“排球”项目达标人数的增长率是多少?
参考答案:
【答案】
(1)600
(2)144°
(3)解:∵第一次模拟测验中,“排球”项目达标的人数为:600×35%=210,
又在第二次模拟测验中,“排球”项目达标的人数增长到了231人,
∴“排球”项目达标人数的增长率是: ![]() ×100%=10%
×100%=10%
【解析】解:(1)150÷25%=600.
即在九年级学生中,达标的总人数是600;
(2)360°×(1﹣35%﹣25%)=144°.
即在扇形统计图中,表示“其他”项目扇形的圆心角的度数是144°;
(3)∵第一次模拟测验中,“排球”项目达标的人数为:600×35%=210,
又在第二次模拟测验中,“排球”项目达标的人数增长到了231人,
∴“排球”项目达标人数的增长率是: ![]() ×100%=10%。
×100%=10%。
所以答案是:(1)600;(2)144°;(3)10%.
【考点精析】本题主要考查了扇形统计图和条形统计图的相关知识点,需要掌握能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况;能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 市首批一次性投放公共自行车700辆供市民租用出行,由于投入数量不够, 导致出现需要租用却未租到车的现象,现随机抽取的某五天在同一时段的调查数据汇成如下表格.
市首批一次性投放公共自行车700辆供市民租用出行,由于投入数量不够, 导致出现需要租用却未租到车的现象,现随机抽取的某五天在同一时段的调查数据汇成如下表格.请回答下列问题:
时间
第一天7:00﹣8:00
第二天7:00﹣8:00
第三天7:00﹣8:00
第四天7:00﹣8:00
第五天7:00﹣8:00
需要租用自行车却未租到车的人数(人)
1500
1200
1300
1300
1200
(1)表格中的五个数据(人数)的中位数是多少?
(2)由随机抽样估计,平均每天在7:00-8:00 :需要租用公共自行车的人数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某体育老师测量了自己任教的甲、乙两班男生的身高,并制作了如下不完整的统计图表
身高分组
频数
频率
152≤ x<155
3
0.06
155≤ x<158
7
0.14
158≤ x<161
m
0.28
161≤ x<164
13
n
164≤ x<167
9
0.18
167≤ x<170
3
0.06
170≤ x<173
1
0.02

根据以上统计图表完成下列问题:
(1)统计表中m=____,n=____;并将频数分布直方图补充完整;
(2)在这次测量中两班男生身高的中位数在什么范围内?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣15﹣
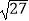 +2cos30°+(π﹣3.14)0+|﹣
+2cos30°+(π﹣3.14)0+|﹣ 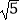 |.
|. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD、DEFG都是正方形,连接AE,CG.
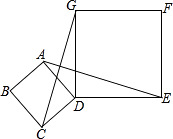
(1)求证:AE=CG;
(2)观察图形,猜想AE与CG之间的位置关系,并证明你的猜想. -
科目: 来源: 题型:
查看答案和解析>>【题目】为倡导“低碳生活”,常选择以自行车作为代步工具.如图1所示是一辆自行车的实物图,车架档AC与CD的长分别为45cm,60cm,且它们互相垂直,座杆CE的长为20cm,车轮半径28cm,点A,C,E在同一条直线上,且∠CAB=75°,如图2
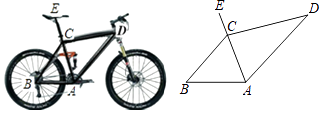
(1)求车座点E到地面的距离;(结果精确到1cm)
(2)求车把点D到车架档直线AB的距离.(结果精确到1cm). -
科目: 来源: 题型:
查看答案和解析>>【题目】某森林公园从正门到侧门有一条公路供游客运动,甲徒步从正门出发匀速走向侧门,出发一段时间开始休息,休息了0.6小时后仍按原速继续行走.乙与甲同时出发,骑自行车从侧门匀速前往正门,到达正门后休息0.2小时,然后按原路原速匀速返回侧门.图中折线分别表示甲、乙到侧门的路程y(km)与甲出发时间x(h)之间的函数关系图象.根据图象信息解答下列问题.
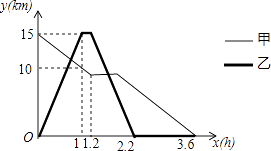
(1)求甲在休息前到侧门的路程y(km)与出发时间x(h)之间的函数关系式.
(2)求甲、乙第一次相遇的时间.
(3)直接写出乙回到侧门时,甲到侧门的路程.
相关试题

