【题目】如图,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=4,BD=5,那么点D到BC的距离是 . 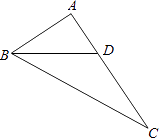
参考答案:
【答案】3
【解析】解:过点D作DE⊥BC于E, 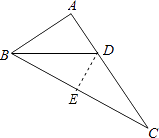
∵在Rt△ABC中,∠A=90°,BD平分∠ABC,
即AD⊥BA,
∴DE=AD,
∵在Rt△ABD中,∠A=90°,AB=4,BD=5,
∴AD= ![]() =3,
=3,
∴DE=AD=3,
∴点D到BC的距离是3.
所以答案是:3.
【考点精析】关于本题考查的角平分线的性质定理和勾股定理的概念,需要了解定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,若点A关于CD所在直线的对称点E恰好为AB的中点,则∠B的度数是( )
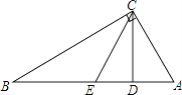
A.60°
B.45°
C.30°
D.75° -
科目: 来源: 题型:
查看答案和解析>>【题目】关于的一元二次方程
 的实数解是
的实数解是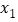 和
和 .
.(1)求
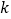 的取值范围;
的取值范围;(2)如果
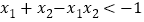 且
且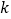 为整数,求
为整数,求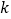 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】把方程2x+y=3改写成用含x的式子表示y的形式,得y= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题14分)如图,点A和动点P在直线
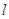 上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O。点C在点P右侧,PC=4,过点C作直线
上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O。点C在点P右侧,PC=4,过点C作直线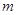 ⊥
⊥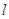 ,过点O作OD⊥
,过点O作OD⊥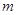 于点D,交AB右侧的圆弧于点E。在射线CD上取点F,使DF=
于点D,交AB右侧的圆弧于点E。在射线CD上取点F,使DF=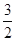 CD,以DE,DF为邻边作矩形DEGF,设AQ=
CD,以DE,DF为邻边作矩形DEGF,设AQ=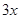
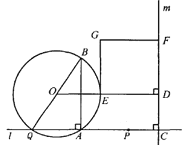
(1)用关于
 的代数式表示BQ,DF;
的代数式表示BQ,DF;(2)当点P在点A右侧时,若矩形DEGF的面积等于90,求AP的长;
(3)在点P的整个运动过程中,
①当AP为何值时,矩形DEGF是正方形?
②作直线BG交⊙O于另一点N,若BN的弦心距为1,求AP的长(直接写出答案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC=26,BC=20,AD是BC边上的中线,AD=24,F是AD上的动点,E是AC边上的动点,则CF+EF的最小值为 .
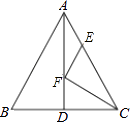
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l:y=
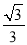 x,点A1(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交y轴于点A2;再过点A2作y轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交y轴于点A3,…,按此作法进行下去,则OA2017=_____.
x,点A1(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交y轴于点A2;再过点A2作y轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交y轴于点A3,…,按此作法进行下去,则OA2017=_____.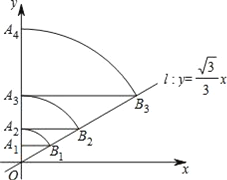
相关试题

