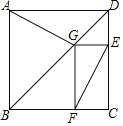
【题目】如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F,若小敏行走的路程为3100m,则小聪行走的路程为( )m.
A.3100B.4600C.3000D.3600
参考答案:
【答案】B
【解析】
连接CG,由正方形的对称性,易知AG=CG,由正方形的对角线互相平分一组对角,GE⊥DC,易得DE=GE.在矩形GECF中,EF=CG.要计算小聪走的路程,只要得到小聪比小敏多走了多少就行.
连接GC,

∵四边形ABCD为正方形,
所以AD=DC,∠ADB=∠CDB=45°,
∵∠CDB=45°,GE⊥DC,
∴△DEG是等腰直角三角形,
∴DE=GE.
在△AGD和△GDC中,
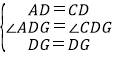 ,
,
∴△AGD≌△GDC(SAS)
∴AG=CG,
在矩形GECF中,EF=CG,
∴EF=AG.
∵BA+AD+DE+EF-BA-AG-GE,
=AD=1500m.
∵小敏共走了3100m,
∴小聪行走的路程为3100+1500=4600(m),
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DB∥AC,且DB=
 AC,E是AC的中点,
AC,E是AC的中点,(1)求证:BC=DE;
(2)连接AD、BE,若要使四边形DBEA是矩形,则给△ABC添加什么条件,为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC=5,cos∠ABC=
 ,将△ABC绕点C顺时针旋转,得到△A1B1C.
,将△ABC绕点C顺时针旋转,得到△A1B1C.(1)如图①,当点B1在线段BA延长线上时.①求证:BB1∥CA1;②求△AB1C的面积;

(2)如图②,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1,求线段EF1长度的最大值与最小值的差.

-
科目: 来源: 题型:
查看答案和解析>>【题目】数学李老师选派了班上8位同学去参加年级组的数学知识竞赛,试卷满分100分,我们将成绩中超过90分的部分记为正,低于90分的部分记为负,则这8位同学的得分如下(单位:分):
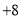 ,
,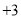 ,
,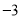 ,
,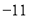 ,
, ,
,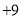 ,
,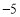 ,
,
(1)请求出这8位同学本次数学竞赛成绩的平均分是多少?
(2)若得95分以上可以获得一等奖,请求出获得一等奖的百分比是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
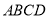 的面积为20cm2,对角线交于点
的面积为20cm2,对角线交于点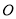 ,以AB、AO为邻边作平行四边形
,以AB、AO为邻边作平行四边形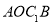 ,对角线交于点
,对角线交于点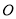 ;以
;以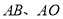 为邻边作平行四边形
为邻边作平行四边形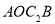 ;…;依此类推,则平行四边形
;…;依此类推,则平行四边形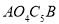 的面积为______,平行四边形
的面积为______,平行四边形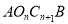 的面积为______.
的面积为______.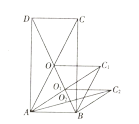
-
科目: 来源: 题型:
查看答案和解析>>【题目】“囧”(jiong)是近时期网络流行语,像一个人脸郁闷的神情.如图所示,一张边长为20的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为
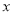 、
、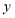 ,剪去的两个小直角三角形的两直角边长也分别为
,剪去的两个小直角三角形的两直角边长也分别为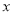 、
、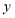 .
.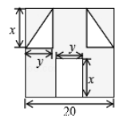
(1)用含有
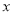 、
、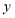 的代数式表示上图中“囧”的面积;
的代数式表示上图中“囧”的面积;(2)当
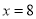 ,
,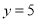 时,求此时“囧”的面积.
时,求此时“囧”的面积. -
科目: 来源: 题型:
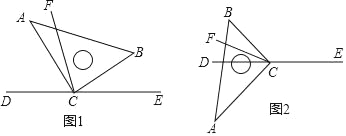
查看答案和解析>>【题目】直角三角板ABC的直角顶点C在直线DE上,CF平分∠BCD.
(1)在图1中,若∠BCE=40°,求∠ACF的度数;
(2)在图1中,若∠BCE=α,直接写出∠ACF的度数(用含α的式子表示);
(3)将图1中的三角板ABC绕顶点C旋转至图2的位置,探究:写出∠ACF与∠BCE的度数之间的关系,并说明理由.
相关试题

