【题目】在△ABC中,AB=AC=5,cos∠ABC=![]() ,将△ABC绕点C顺时针旋转,得到△A1B1C.
,将△ABC绕点C顺时针旋转,得到△A1B1C.
(1)如图①,当点B1在线段BA延长线上时.①求证:BB1∥CA1;②求△AB1C的面积;

(2)如图②,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1,求线段EF1长度的最大值与最小值的差.

参考答案:
【答案】(1)①证明见试题解析;②![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)①根据旋转的性质和平行线的性质证明;
②过A作AF⊥BC于F,过C作CE⊥AB于E,根据等腰三角形的性质和三角形的面积公式解答;
(2)过C作CF⊥AB于F,以C为圆心CF为半径画圆交BC于F1,和以C为圆心BC为半径画圆交BC的延长线于F1,得出最大和最小值解答即可.
试题解析:(1)①证明:∵AB=AC,B1C=BC,
∴∠AB1C=∠B,∠B=∠ACB,
∵∠AB1C=∠ACB(旋转角相等),
∴∠B1CA1=∠AB1C,
∴BB1∥CA1;
②过A作AF⊥BC于F,过C作CE⊥AB于E,如图1:
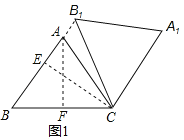
∵AB=AC,AF⊥BC,BC=6,
∴BF=CF=3,
∴B1C=BC=6,
可得:B1B=2BE,
∵EC=![]() ,
,
∴BE=![]() ,则BB1=
,则BB1=![]() ,
,
故AB1=![]() ﹣5=
﹣5=![]() ,
,
∴△AB1C的面积为:![]() ;
;
(2)如图2,过C作CF⊥AB于F,以C为圆心CF为半径画圆交BC于F1,EF1有最小值,
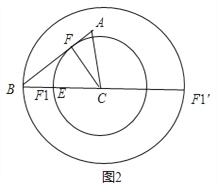
此时在Rt△BFC中,CF=![]() ,
,
∴CF1=![]() ,
,
∴EF1的最小值为![]() ﹣3=
﹣3=![]() ;
;
如图,以C为圆心BC为半径画圆交BC的延长线于F1,EF1有最大值;
此时EF1=EC+CF1=3+6=9,
∴线段EF1的最大值与最小值的差为9﹣![]() =
=![]() .
.
-
科目: 来源: 题型:
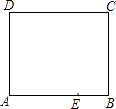
查看答案和解析>>【题目】如图是一张长方形纸片ABCD,已知AB=8,AD=7,E为AB上一点,AE=5,现要剪下一张等腰三角形纸片(△AEP),使点P落在长方形ABCD的某一条边上,则等腰三角形AEP的底边长是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列算式:21=2、22=4、23=8、24=16、25=32、26=64、27=128、28=256….观察后,用你所发现的规律写出223的末位数字是 .
-
科目: 来源: 题型:
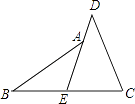
查看答案和解析>>【题目】阅读下面的题目及分析过程,并按要求进行证明. 已知:如图,E是BC的中点,点A在DE上,且∠BAE=∠CDE.
求证:AB=CD.
分析:证明两条线段相等,常用的一般方法是应用全等三角形或等腰三角形的判定和性质,观察本题中要证明的两条线段,它们不在同一个三角形中,且它们分别所在的两个三角形也不全等.因此,要证AB=CD,必须添加适当的辅助线,构造全等三角形或等腰三角形.
现给出如下三种添加辅助线的方法,请任意选择其中一种,对原题进行证明.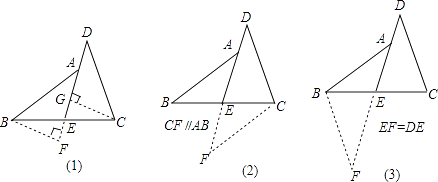
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工程队由甲乙两队组成,承包我市河东东街改造工程,规定若干天完成,已知甲单独完成这项工程所需时间比规定时间多32天,乙队单独完成这项工程所需时间比规定时间多12天,如果甲乙两队先合作20天,剩下的甲单独做,则延误两天完成,那么规定时间是多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中结果正确的是( )
A.aa2=a2B.a2÷a=2C.2a2+a2=3a4D.(﹣a)3=﹣a3
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:5 – x = 18
相关试题

