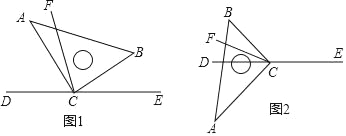
【题目】直角三角板ABC的直角顶点C在直线DE上,CF平分∠BCD.
(1)在图1中,若∠BCE=40°,求∠ACF的度数;
(2)在图1中,若∠BCE=α,直接写出∠ACF的度数(用含α的式子表示);
(3)将图1中的三角板ABC绕顶点C旋转至图2的位置,探究:写出∠ACF与∠BCE的度数之间的关系,并说明理由.
参考答案:
【答案】(1)∠ACF=20°;(2)∠ACF=![]() α;(3)∠ACF=
α;(3)∠ACF=![]() ∠BCE.理由见解析.
∠BCE.理由见解析.
【解析】试题分析:(1)由∠ACB=90°,∠BCE=40°,可得∠ACD,∠BCD的度数,再根据CF平分∠BCD,可得∠DCF的度数,继而可求得∠ACF=∠DCF﹣∠ACD=20°;
(2)由∠ACB=90°,∠BCE=α°,可得∠ACD=90°﹣α,∠BCD=180°﹣α,再根据CF平分∠BCD,从而可得∠DCF=90°﹣![]() α,继而可得∠ACF=
α,继而可得∠ACF=![]() α;
α;
(3)由点C在DE上,可得∠BCD=180°﹣∠BCE,再根据CF平分∠BCD,可得∠BCF=90°-![]() ∠BCE,再根据∠ACB=90°,从而有∠ACF=
∠BCE,再根据∠ACB=90°,从而有∠ACF=![]() ∠BCE.
∠BCE.
试题解析:(1)如图1,∵∠ACB=90°,∠BCE=40°,
∴∠ACD=180°﹣90°﹣40°=50°,∠BCD=180°﹣40°=140°,
又CF平分∠BCD,
∴∠DCF=∠BCF=![]() ∠BCD=70°,
∠BCD=70°,
∴∠ACF=∠DCF﹣∠ACD=70°﹣50°=20°;
(2)如图1,∵∠ACB=90°,∠BCE=α°,
∴∠ACD=180°﹣90°﹣α°=90°﹣α,∠BCD=180°﹣α,
又CF平分∠BCD,
∴∠DCF=∠BCF=![]() ∠BCD=90°﹣
∠BCD=90°﹣![]() α,
α,
∴∠ACF=90°﹣![]() α﹣90°+α=
α﹣90°+α=![]() α;
α;
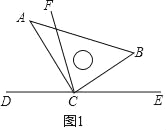
(3)∠ACF=![]() ∠BCE.理由如下:
∠BCE.理由如下:
如图2,∵点C在DE上,
∴∠BCD=180°﹣∠BCE.
∵CF平分∠BCD,
∴∠BCF=![]() ∠BCD=
∠BCD=![]() (180°﹣∠BCE)=90°-
(180°﹣∠BCE)=90°-![]() ∠BCE.
∠BCE.
∵∠ACB=90°,
∴∠ACF=∠ACB﹣∠BCF=90°﹣(90°-![]() ∠BCE)=
∠BCE)=![]() ∠BCE.
∠BCE.
即:∠ACF=![]() ∠BCE.
∠BCE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F,若小敏行走的路程为3100m,则小聪行走的路程为( )m.
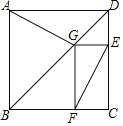
A.3100B.4600C.3000D.3600
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
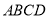 的面积为20cm2,对角线交于点
的面积为20cm2,对角线交于点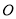 ,以AB、AO为邻边作平行四边形
,以AB、AO为邻边作平行四边形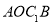 ,对角线交于点
,对角线交于点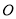 ;以
;以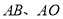 为邻边作平行四边形
为邻边作平行四边形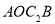 ;…;依此类推,则平行四边形
;…;依此类推,则平行四边形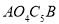 的面积为______,平行四边形
的面积为______,平行四边形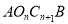 的面积为______.
的面积为______.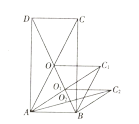
-
科目: 来源: 题型:
查看答案和解析>>【题目】“囧”(jiong)是近时期网络流行语,像一个人脸郁闷的神情.如图所示,一张边长为20的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为
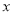 、
、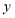 ,剪去的两个小直角三角形的两直角边长也分别为
,剪去的两个小直角三角形的两直角边长也分别为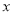 、
、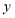 .
.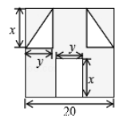
(1)用含有
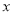 、
、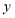 的代数式表示上图中“囧”的面积;
的代数式表示上图中“囧”的面积;(2)当
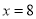 ,
,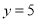 时,求此时“囧”的面积.
时,求此时“囧”的面积. -
科目: 来源: 题型:
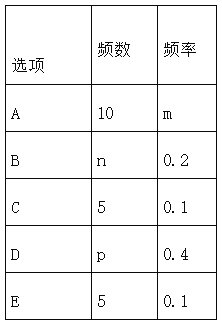
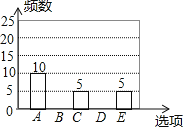
查看答案和解析>>【题目】随着移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选项:A.和同学亲友聊天;B.学习;C.购物;D.游戏;E.其它),端午节后某中学在全校范围内随机抽取了若干名学生进行调查,得到图表(部分信息未给出):
根据以上信息解答下列问题:
(1)这次被调查的学生有多少人?
(2)求表中m,n,p的值,并补全条形统计图.
(3)若该中学约有800名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?并根据以上调查结果,就中学生如何合理使用手机给出你的一条建议.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,菱形ABCD中,AB=5cm,动点P从点B出发,沿折线BC﹣CD﹣DA运动到点A停止,动点Q从点A出发,沿线段AB运动到点B停止,它们运动的速度相同,设点P出发xs时,△BPQ的面积为ycm2 , 已知y与x之间的函数关系如图②所示,其中OM,MN为线段,曲线NK为抛物线的一部分,请根据图中的信息,解答下列问题:

(1)当1<x<2时,△BPQ的面积________(填“变”或“不变”);
(2)分别求出线段OM,曲线NK所对应的函数表达式;
(3)当x为何值时,△BPQ的面积是5cm2?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两列火车分别从A、B两城同时匀速驶出,甲车开往B城,乙车开往A城.由于墨迹遮盖,图中提供的是两车距B城的路程S甲(千米)、S乙(千米)与行驶时间t(时)的函数图象的一部分.
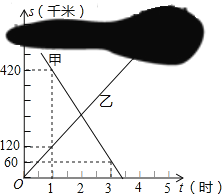
(1)分别求出S甲、S乙与t的函数关系式(不必写出t的取值范围);
(2)求A、B两城之间的距离,及t为何值时两车相遇;
(3)当两车相距300千米时,求t的值.
相关试题

