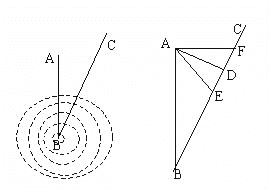
【题目】如图,正方形ABCD的边长为4厘米,动点P从点A出发沿AB边由A向B以1厘米/秒的速度匀速移动(点P不与点A、B重合),动点Q从点B出发沿拆线BC-CD以2厘米/秒的速度匀速移动。点P、Q同时出发,当点P停止运动,点Q也随之停止。联结AQ交BD于点E。设点P运动时间为t秒。
(1)用t表示线段PB的长;
(2)当点Q在线段BC上运动时,t为何值时,∠BEP和∠BEQ相等;
(3)当t为何值时,线段P、Q之间的距离为2![]() cm.
cm.

参考答案:
【答案】(1)PB=4-t;(2)t=![]() ;(3)t=2或
;(3)t=2或![]() ;
;
【解析】
(1)根据正方形的性质和已知条件即可求解;(2)由正方形的性质得出∠PBE=∠QBE,再证明△BEP≌△BEQ,根据全等三角形的性质可得BP=BQ,即可得出方程4-t=2t,解方程即可求得t值;(3)分两种情况讨论:①当![]() 时和②当
时和②当![]() 时,根据已知条件,利用勾股定理得出方程,解方程即可求得t的值.
时,根据已知条件,利用勾股定理得出方程,解方程即可求得t的值.
(1)PB=AB-AP,
∵AB=4,AP=1×t=t,
∴PB=4-t.
(2)当t=![]() 时,∠BEP和∠BEQ相等,理由如下:
时,∠BEP和∠BEQ相等,理由如下:
∵四边形ABCD正方形,
∴ 对角线BD平分∠ABC,
∴∠PBE=∠QBE,
当∠BEP=∠BEQ 时,
在△BEP和△BEQ中,
 ,
,
∴△BEP≌△BEQ,
∴BP=BQ,
即4-t=2t,
解得t=![]() ;
;
(3)分两种情况讨论:
①当![]() 时,即当P点在AB上,Q点在BC上运动时,
时,即当P点在AB上,Q点在BC上运动时,
连接PQ,如图1所示:

根据勾股定理得:![]() ,
,
即![]()
解得t=2或t=![]() (负值舍去);
(负值舍去);
②当![]() 时,即当P点在AB上,Q点在CD上运动时,
时,即当P点在AB上,Q点在CD上运动时,
作PM⊥CD于M,如图2所示:
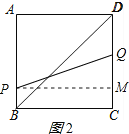
∴PM=BC=4,CM=BP=4-t,MQ=2t-4-(4-t)=3t-8,
根据勾股定理得:![]() ,
,
即![]()
解得t=2(舍去)或t=![]() ;
;
综上,当t=2或t=![]() 时,PQ之间的距离为2
时,PQ之间的距离为2![]() cm.
cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读并填空:
寻求某些勾股数的规律:
⑴对于任何一组已知的勾股数都扩大相同的正整数倍后,就得到了一组新的勾股数.例如:
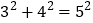 ,我们把它扩大2倍、3倍,就分别得到
,我们把它扩大2倍、3倍,就分别得到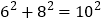 和
和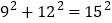 ,……若把它扩大11倍,就得到 ,若把它扩大n倍,就得到 .
,……若把它扩大11倍,就得到 ,若把它扩大n倍,就得到 .⑵对于任意一个大于1的奇数,存在着下列勾股数:
若勾股数为3,4,5,因为,则有
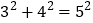 ;
;若勾股数为5,12,13,则有
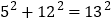 ;
;若勾股数为7,24,25,则有 ;……
若勾股数为m(m为奇数),n, ,则有m2= ,用m来表示n= ;
当m=17时,则n= ,此时勾股数为 .
⑶对于大于4的偶数:
若勾股数为6,8,10,因为
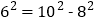 ,则有……请找出这些勾股数之间的关系,并用适当的字母表示出它的规律来,并求当偶数为24的勾股数.
,则有……请找出这些勾股数之间的关系,并用适当的字母表示出它的规律来,并求当偶数为24的勾股数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AC为对角线,点E、F分别是边BC、AD的中点.
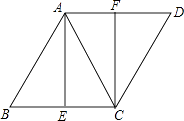
(1)求证:△ABE≌△CDF;
(2)若∠B=60°,AB=4,求线段AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】台风是一种自然灾害,它以台风中心为圆心在周围数十千米范围内形成气旋风暴,有极强的破坏力,如图,据气象观测,距沿海某城市A的正南方向220千米B处有一台风中心,其中心最大风力为12级,每远离台风中心20千米,风力就会减弱一级,该台风中心现正以15千米/时的速度沿北偏东30方向往C移动,且台风中心风力不变,若城市所受风力达到或走过四级,则称为受台风影响.
(1)该城市是否会受到这交台风的影响?请说明理由.
(2)若会受到台风影响,那么台风影响该城市持续时间有多少?
(3)该城市受到台风影响的最大风力为几级?
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们定义三个有理数之间的新运算法则“⊕”:a⊕b⊕c=
 (|a﹣b﹣c|+a+b+c),如:1⊕(﹣2)⊕3=
(|a﹣b﹣c|+a+b+c),如:1⊕(﹣2)⊕3= [|1﹣(﹣2)﹣3|+1+(﹣2)+3]=l,在﹣2,﹣4,﹣5,0,2,5,6这7个数中,任意取三个数作为a,b,c的值,进行“a⊕b⊕c“运算,求在所有计算的结果中的最大值是_____.
[|1﹣(﹣2)﹣3|+1+(﹣2)+3]=l,在﹣2,﹣4,﹣5,0,2,5,6这7个数中,任意取三个数作为a,b,c的值,进行“a⊕b⊕c“运算,求在所有计算的结果中的最大值是_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上,点A表示数a,点B表示数b,在学习绝对值时,我们知道了绝对值的几何含义:
数轴上A、B之间的距离记作|AB|,定义:|AB|=|a﹣b|.如:|a+6|表示数a和﹣6在数轴上对应的两点之间的距离.|a﹣1|表示数a和1在数轴上对应的两点之间的距离.
(1)若a满足|a+6|+|a+4|+|a﹣1|的值最小,b与3a互为相反数,直接写出点A对应的数 ,点B对应的数 .
(2)在(1)的条件下,已知点E从点A出发以1单位/秒的速度向右运动,同时点F从点B出发以2单位/秒的速度向右运动,FO的中点为点P,则下列结论:①PO+AE的值不变;②PO﹣AE的值不变,其中有且只有一个是正确的,选出来并求其值.
(3)在(1)的条件下,已知动点M从A点出发以1单位/秒的速度向左运动,动点N从B点出发以3单位/秒的速度向左运动,动点T从原点的位置出发以x单位/秒的速度向左运动,三个动点同时出发,若运动过程中正好先后出现两次TM=TN的情况,且两次间隔的时间为4秒,求满足条件的x的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:A=2x2+ax﹣5y+b,B=bx2﹣
 x﹣
x﹣ y﹣3.
y﹣3.(1)求3A﹣(4A﹣2B)的值;
(2)当x取任意数值,A﹣2B的值是一个定值时,求(a+
 A)﹣(2b+
A)﹣(2b+ B)的值.
B)的值.
相关试题

