【题目】在数轴上,点A表示数a,点B表示数b,在学习绝对值时,我们知道了绝对值的几何含义:
数轴上A、B之间的距离记作|AB|,定义:|AB|=|a﹣b|.如:|a+6|表示数a和﹣6在数轴上对应的两点之间的距离.|a﹣1|表示数a和1在数轴上对应的两点之间的距离.
(1)若a满足|a+6|+|a+4|+|a﹣1|的值最小,b与3a互为相反数,直接写出点A对应的数 ,点B对应的数 .
(2)在(1)的条件下,已知点E从点A出发以1单位/秒的速度向右运动,同时点F从点B出发以2单位/秒的速度向右运动,FO的中点为点P,则下列结论:①PO+AE的值不变;②PO﹣AE的值不变,其中有且只有一个是正确的,选出来并求其值.
(3)在(1)的条件下,已知动点M从A点出发以1单位/秒的速度向左运动,动点N从B点出发以3单位/秒的速度向左运动,动点T从原点的位置出发以x单位/秒的速度向左运动,三个动点同时出发,若运动过程中正好先后出现两次TM=TN的情况,且两次间隔的时间为4秒,求满足条件的x的值.

参考答案:
【答案】(1)点A对应的数﹣4,点B对应的数12;(2)PO﹣AE的值不变;(3)满足条件的x的值为2
【解析】
(1)a满足|a+6|+|a+4|+|a﹣1|的值最小,所以数a和﹣6,a和﹣4,a和1在数轴上对应的两点之间的距离之和最小,所以a=﹣4,b=12;(2)设运动时间为t秒,根据题意计算出PO和AE的长,进行计算即可;(3)设运动时间为t秒,根据两次TM=TN,且间隔的时间为4秒,列出方程组即可.
(1)a满足|a+6|+|a+4|+|a﹣1|的值最小,所以数a和﹣6,a和﹣4,a和1在数轴上对应的两点之间的距离之和最小,
∴a=﹣4,b=12
∴点A对应的数﹣4,点B对应的数12
(2)PO﹣AE的值不变
设运动时间为t秒,根据题意可得:BF=2t,AE=t,则OF=12+2t
∵FO的中点为点P
∴OP=6+t
∴PO﹣AE=6+t﹣t=6
PO﹣AE的值不变
(3)设运动时间为t秒,则AM=t,OT=xt,BN=3t
根据第一次TM=TN得:xt+12﹣3t=4+t﹣xt
根据第二次TM=TN得:x(t+4)﹣{3(t+4)﹣12}=4+(4+t)﹣x(4+t)
两式联立得:x=2
∴满足条件的x的值为2
-
科目: 来源: 题型:
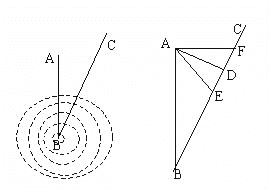
查看答案和解析>>【题目】台风是一种自然灾害,它以台风中心为圆心在周围数十千米范围内形成气旋风暴,有极强的破坏力,如图,据气象观测,距沿海某城市A的正南方向220千米B处有一台风中心,其中心最大风力为12级,每远离台风中心20千米,风力就会减弱一级,该台风中心现正以15千米/时的速度沿北偏东30方向往C移动,且台风中心风力不变,若城市所受风力达到或走过四级,则称为受台风影响.
(1)该城市是否会受到这交台风的影响?请说明理由.
(2)若会受到台风影响,那么台风影响该城市持续时间有多少?
(3)该城市受到台风影响的最大风力为几级?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为4厘米,动点P从点A出发沿AB边由A向B以1厘米/秒的速度匀速移动(点P不与点A、B重合),动点Q从点B出发沿拆线BC-CD以2厘米/秒的速度匀速移动。点P、Q同时出发,当点P停止运动,点Q也随之停止。联结AQ交BD于点E。设点P运动时间为t秒。
(1)用t表示线段PB的长;
(2)当点Q在线段BC上运动时,t为何值时,∠BEP和∠BEQ相等;
(3)当t为何值时,线段P、Q之间的距离为2
 cm.
cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们定义三个有理数之间的新运算法则“⊕”:a⊕b⊕c=
 (|a﹣b﹣c|+a+b+c),如:1⊕(﹣2)⊕3=
(|a﹣b﹣c|+a+b+c),如:1⊕(﹣2)⊕3= [|1﹣(﹣2)﹣3|+1+(﹣2)+3]=l,在﹣2,﹣4,﹣5,0,2,5,6这7个数中,任意取三个数作为a,b,c的值,进行“a⊕b⊕c“运算,求在所有计算的结果中的最大值是_____.
[|1﹣(﹣2)﹣3|+1+(﹣2)+3]=l,在﹣2,﹣4,﹣5,0,2,5,6这7个数中,任意取三个数作为a,b,c的值,进行“a⊕b⊕c“运算,求在所有计算的结果中的最大值是_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:A=2x2+ax﹣5y+b,B=bx2﹣
 x﹣
x﹣ y﹣3.
y﹣3.(1)求3A﹣(4A﹣2B)的值;
(2)当x取任意数值,A﹣2B的值是一个定值时,求(a+
 A)﹣(2b+
A)﹣(2b+ B)的值.
B)的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件个数:
每人加工零件个数
540
450
300
240
210
120
人数
1
1
2
6
3
2
(1)写出这15人该月加工零件数的平均数、中位数和众数.
(2)假如生产部负责人把每位工人的月加工零件个数定为260,你认为这个定额是否合理?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某旅游景区上山的一条小路上,有一些断断续续的台阶.下图是其中的甲、乙两段台阶路的示意图.请你用所学过的有关统计知识(平均数、中位数、方差和极差)回答下列问题:
(1)两段台阶路有哪些相同点和不同点?
(2)哪段台阶路走起来更舒服?为什么?
(3)为方便游客行走,需要重新整修上山的小路.对于这两段台阶路,在台阶数不变的情况下,请你提出合理的整修建议.
图中的数字表示每一级台阶的高度(单位:cm),并且数据15,16,16,14,14,15的方差s甲2=
 ,数据11,15,18,17,10,19的方差s乙2=
,数据11,15,18,17,10,19的方差s乙2= .
.
相关试题

