【题目】海珠区某学校为进一步加强和改进学校体育工作,切实提高学生体质健康水平,决定推进“一人一球”活动计划. 学生可根据自己的喜好选修一门球类项目(A :足球,B:篮球,C:排球,D:羽毛球,E:乒乓球),陈老师对某班全班同学的
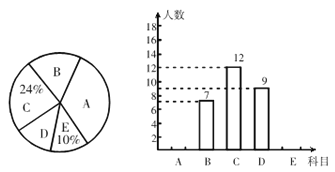
选课情况进行统计后,制成了两幅不完整的统计图 (如图).
(1) 求出该班的总人数,并将条形统计图补充完整;
(2) 若该校共有学生 2500 名,请估计约有多少人选修足球?
(3) 该班班委 4 人中,1 人选修足球,1 人选修篮球,2 人选修羽毛球,陈老师要从这
4 人中任选 2 人了解他们对体育选修课的看法,请你用列表或画树状图的方法,求 选出的 2 人中至少有 1 人选修羽毛球的概率.
参考答案:
【答案】(1)见解析(2)850(3)![]()
【解析】分析:(1)、先利用C的人数和所占的百分比计算出全班人数,再利用E的百分比计算出E的人数,则用全班人数分别减去B、C、D、E的人数得到A的人数,补全统计图即可.
(2)根据样本估计总体,用![]() 表示全校学生对足球感兴趣的百分比,然后用2500乘以
表示全校学生对足球感兴趣的百分比,然后用2500乘以![]() 即可得到选修足球的人数;
即可得到选修足球的人数;
(4)先利用树状图展示所有12种等可能的结果数,找出选出的![]() 人至少1人选修羽毛球所占结果数,然后根据概率公式求解.
人至少1人选修羽毛球所占结果数,然后根据概率公式求解.
详解:(1)该班总人数是:该班人数为12÷24%=50(人),
答:该班总人数是50人.
则E类人数是:10%×50=5(人),
A类人数为:5071295=17(人),
补全条形统计图如图所示:
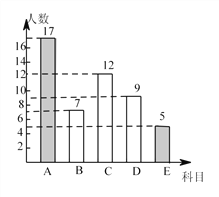
(2)选修足球的人数:![]() (人),
(人),
答:该校约有850人选修足球.
(3)用“ ![]() ”代表选修足球的1人,用“B ”代表选修篮球的1人,用“D1、D2”代表选修足球的2人,根据题意画出树状图如下:
”代表选修足球的1人,用“B ”代表选修篮球的1人,用“D1、D2”代表选修足球的2人,根据题意画出树状图如下:
由图可以看出,可能出现的结果有12种,并且它们出现的可能性相等.
其中至少1人选修羽毛球的结果有10种,
所以至少有 1 人选修羽毛球的概率![]()
答:选出的![]() 人至少1人选修羽毛球的概率为
人至少1人选修羽毛球的概率为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为解决部分市民冬季集中取暖问题,需铺设一条长4000米的管道,为尽量减少施工对交通造成的影响,施工时“…”,设实际每天铺设管道x米,则可得方程
 =20,根据此情景,题中用“…”表示的缺失的条件应补为( )
=20,根据此情景,题中用“…”表示的缺失的条件应补为( )A. 每天比原计划多铺设10米,结果延期20天完成
B. 每天比原计划少铺设10米,结果延期20天完成
C. 每天比原计划多铺设10米,结果提前20天完成
D. 每天比原计划少铺设10米,结果提前20天完成
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知P为正方形ABCD外的一点,PA=1,PB=2,将△ABP绕点B顺时针旋转90°,使点P旋转至点P′,且AP′=3,则∠BP′C的度数为 ( )
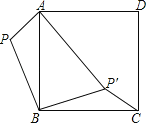
A.105° B.112.5° C.120° D.135°
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形 A BCD 中,对角线 A C、BD 相交于点 O,DE 平分∠A DO 交 AC 于点 E ,把
 A DE 沿AD 翻折,得到
A DE 沿AD 翻折,得到 A DE’,点 F 是 DE 的中点,连接 A F、BF、E’F,若 AE=
A DE’,点 F 是 DE 的中点,连接 A F、BF、E’F,若 AE= .
.下列结论 :①AD 垂直平分 EE’,② tan∠ADE =
 -1,
-1, ③ C
 A DE - C
A DE - C ODE =2
ODE =2 -1, ④ S四边形AEFE=
-1, ④ S四边形AEFE= 
其中结论正确的个数是 ( ) .

A. 4 个 B. 3 个 C. 2 个 D. 1 个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C在线段AB上,AC=8 cm,CB=6 cm,点M,N分别是AC,BC的中点.
(1)求线段MN的长.
(2)若C为线段AB上任一点,满足AC+CB=a cm,其他条件不变,你能猜想MN的长度吗?(用含a的代数式表示)并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数 y=k x+b 与反比例函数
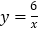 图象交于点 A (2,m) 和点 B(n,-2).
图象交于点 A (2,m) 和点 B(n,-2).(1) 求此一次函数解析式及m、n的值;
(2) 结合图象求不等式
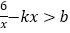 的解集.
的解集.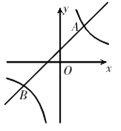
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 相交于
相交于 ,
, 平分
平分 ,给出下列结论:①当
,给出下列结论:①当 时,
时, ;②
;② 为
为 的平分线;③与
的平分线;③与 相等的角有三个;④
相等的角有三个;④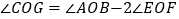 。其中正确的结论有( )
。其中正确的结论有( )
A.
 个B.
个B.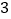 个C.
个C. 个D.
个D. 个
个
相关试题

