【题目】如图,已知正方形ABCD边长为1,∠EAF=45°,AE=AF,则有下列结论:
①∠1=∠2=22.5°;
②点C到EF的距离是 ![]() -1;
-1;
③△ECF的周长为2;
④BE+DF>EF.
其中正确的结论是 . (写出所有正确结论的序号)
参考答案:
【答案】①②③
【解析】解:∵四边形ABCD为正方形,
∴AB=AD,∠BAD=∠B=∠D=90°,
在Rt△ABE和Rt△ADF中![]() ,
,
∴Rt△ABE≌Rt△ADF,
∴∠1=∠2,
∵∠EAF=45°,
∴∠1=∠2=∠22.5°,所以①正确;
连结EF、AC,它们相交于点H,如图,
∵Rt△ABE≌Rt△ADF,
∴BE=DF,
而BC=DC,
∴CE=CF,
而AE=AF,
∴AC垂直平分EF,AH平分∠EAF,
∴EB=EH,FD=FH,
∴BE+DF=EH+HF=EF,所以④错误;
∴△ECF的周长=CE+CF+EF=CED+BE+CF+DF=CB+CD=1+1=2,所以③正确;
设BE=x,则EF=2x,CE=1﹣x,
∵△CEF为等腰直角三角形,
∴EF= ![]() CE,即2x=
CE,即2x= ![]() (1﹣x),解得x=
(1﹣x),解得x= ![]() ﹣1,
﹣1,
∴EF=2( ![]() ﹣1),
﹣1),
∴CH= ![]() EF=
EF= ![]() ﹣1,所以②正确.
﹣1,所以②正确.
故答案为①②③.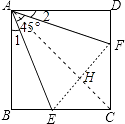
先证明Rt△ABE≌Rt△ADF得到∠1=∠2,易得∠1=∠2=∠22.5°,于是可对①进行判断;连结EF、AC,它们相交于点H,如图,利用Rt△ABE≌Rt△ADF得到BE=DF,则CE=CF,接着判断AC垂直平分EF,AH平分∠EAF,于是利用角平分线的性质定理得到EB=EH,FD=FH,则可对③④进行判断;设BE=x,则EF=2x,CE=1﹣x,利用等腰直角三角形的性质得到2x= ![]() (1﹣x),解得x=
(1﹣x),解得x= ![]() ﹣1,则可对④进行判断.本题考查了四边形的综合题:熟练掌握正方形的性质和角平分线的性质定理.解决本题的关键是证明AC垂直平分EF.
﹣1,则可对④进行判断.本题考查了四边形的综合题:熟练掌握正方形的性质和角平分线的性质定理.解决本题的关键是证明AC垂直平分EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为S1 , 正八边形外侧八个扇形(阴影部分)面积之和为S2 , 则
 =( )
=( ) 
A.
B.
C.
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△AOB的顶点O在直线l上,且AO=AB.

(1)画出△AOB关于直线l成轴对称的图形△COD,且使点A的对称点为点C ;
(2)在(1)的条件下,AC与BD的位置关系是________;
(3)在(1)、(2)的条件下,联结AD,如果∠ABD=2∠ADB,求∠AOC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】同时投掷两个骰子,它们点数之和不大于4的概率是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)请画出△ABC关于y轴对称的△A′B′C′(其中A′,B′,C′分别是A,B,C的对应点,不写画法);
(2)直接写出A′,B′,C′三点的坐标:A′( ),B′( ),C′( )
(3)计算△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】化简:(
 )
)  .
. -
科目: 来源: 题型:
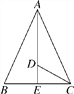
查看答案和解析>>【题目】如图,在△ABC中,已知AB=AC,∠BAC和∠ACB的平分线相交于点D,∠ADC=125°,求∠ACB和∠BAC的度数.
相关试题

