【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于点N,连接BM、DN.

(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长。
参考答案:
【答案】(1)证明见解析;(2)MD长为![]() .
.
【解析】试题分析:(1)根据矩形性质求出AD∥BC,推出∠MDO=∠NBO,∠DMO=∠BNO,证△DMO≌△BNO,推出OM=ON,得出平行四边形BMDN,推出菱形BMDN;
(2)根据菱形性质求出DM=BM,在Rt△AMB中,根据勾股定理得出BM2=AM2+AB2,即可列方程求得.
试题解析:(1)∵四边形ABCD是矩形
∴AD∥BC,∠A=90°,
∴∠MDO=∠NBO,∠DMO=∠BNO,
∵在△DMO和△BNO中
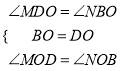
∴△DMO≌△BNO(ASA),
∴OM=ON,
∵OB=OD,
∴四边形BMDN是平行四边形,
∵MN⊥BD,
∴平行四边形BMDN是菱形.
(2)∵四边形BMDN是菱形,
∴MB=MD,
设MD长为x,则MB=DM=x,
在Rt△AMB中,BM2=AM2+AB2
即x2=(4-x)2+22,
解得:x=![]() ,
,
答:MD长为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等边△ABC的边长为4cm,点P,Q分别从B,C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s;
点Q沿CA,AB向终点B运动,速度为2cm/s,设它们运动的时间为x(s),
(1)如图(1),当x为何值时,PQ∥AB;
(2)如图(2),若PQ⊥AC,求x;
(3)如图(3),当点Q在AB上运动时,PQ与△ABC的高AD交于点O,OQ与OP是否总是相等?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a2+a3=a5B.a2a3=a5C.(a2)3=a8D.(ab)2=ab2
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下各组数据为长度的三条线段,能组成三角形的是( )
A.1,2,3B.1,4,3C.5,9,5D.2,7,3
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算x2x2的结果是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)如图,在10×10的正方形网格中,点A,B,C,D均在格点上,以点A为位似中心画四边形AB′C′D′,使它与四边形ABCD位似,且相似比为2.

(1)在图中画出四边形AB′C′D′;
(2)填空:△AC′D′是 三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E是ABCD的对角线AC上任一点,则下列结论不一定成立的是( )

A.S△ABE=S△ADE
B.S△BCE=S△DCE
C.S△ADE+S△BCE= SABCD
SABCD
D.S△ADE<S△BCE
相关试题

