Question

【题目】已知等边△ABC的边长为4cm，点P，Q分别从B，C两点同时出发，其中点P沿BC向终点C运动，速度为1cm/s；
点Q沿CA，AB向终点B运动，速度为2cm/s，设它们运动的时间为x（s），
（1）如图（1），当x为何值时，PQ∥AB；

（2）如图（2），若PQ⊥AC，求x；

（3）如图（3），当点Q在AB上运动时，PQ与△ABC的高AD交于点O，OQ与OP是否总是相等？请说明理由．

Answer 1

【答案】
（1）解：∵∠C=60°，
∴当PC=CQ时，△PQC为等边三角形，
于是∠QPC=60°=∠B，
从而PQ∥AB，
∵PC=4﹣x，CQ=2x，
由4﹣x=2x，
解得：x= ，
∴当x= 时，PQ∥AB
（2）解：∵PQ⊥AC，∠C=60°，
∴∠QPC=30°，
∴CQ= PC，
即2x= （4﹣x），
解得：x=
（3）解：OQ=PO，理由如下：
作QH⊥AD于H，如图（3），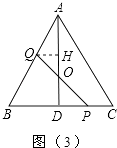

∵AD⊥BC，
∴∠QAH=30°，BD= BC=2，
∴QH= AQ= （2x﹣4）=x﹣2，
∵DP=BP﹣BD=x﹣2，
∴QH=DP，
在△OQH和△OPD中，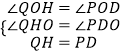
，
∴△OQH≌△OPD（AAS），
∴OQ=OP．
【解析】（1）可从结论入手，若PQ∥AB，可得出△PQC为等边三角形，PC=4﹣x=CQ=2x，进而求出x;（2）利用直角三角形中30度角的性质，得出CQ= PC，求出x;(3)通过Q点作垂线，利用x的代数式表示QH=DP，构造△OQH≌△OPD，进而OQ=OP.