【题目】如图,二次函数![]() .图象的顶点为
.图象的顶点为![]() ,其图象与
,其图象与![]() 轴的交点
轴的交点![]() 、
、![]() 的横坐标分别为
的横坐标分别为![]() 、
、![]() ,与
,与![]() 轴负半轴交于点
轴负半轴交于点![]() .下面五个结论:①
.下面五个结论:①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() 随
随![]() 值的增大而增大;④当
值的增大而增大;④当![]() 时,
时,![]() ;⑤只有当
;⑤只有当![]() 时,
时,![]() 是等腰直角三角形.那么,其中正确的结论______.(只填你认为正确结论的序号)
是等腰直角三角形.那么,其中正确的结论______.(只填你认为正确结论的序号)
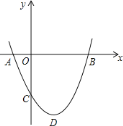
参考答案:
【答案】①⑤
【解析】
根据抛物线的对称性可得到抛物线的对称轴为直线x=1,根据抛物线的对称轴为直线x=﹣![]() =1可判断①正确;根据图象得x=1对应的函数值为负数,可判断以②错误;
=1可判断①正确;根据图象得x=1对应的函数值为负数,可判断以②错误;
根据抛物线当a>0,在对称轴左侧,y随x的增大而减小可判断以③错误;利用x=﹣1或x=3时,ax2+bx+c=0,可判断④错误;设抛物线的解析式为y=a(x+1)(x﹣3)=ax2﹣2ax﹣3a,对称轴x=1交x轴与E点,当△ABD是等腰直角三角形,得到DE=![]() AB,解方程求出a的值即可判断⑤正确.
AB,解方程求出a的值即可判断⑤正确.
∵二次函数的图象与x轴的交点A、B的横坐标分别为﹣1、3,∴AB中点坐标为(1,0),而点A与点B是抛物线上的对称点,∴抛物线的对称轴为直线x=1,∴x=﹣![]() =1,即2a+b=0,所以①正确;
=1,即2a+b=0,所以①正确;
∵当x=1时,对应的函数图象在x轴下方,∴a+b+c<0,所以②错误;
∵a>0,∴当x≤1时,y随x值的增大而减,所以③错误;
由于当﹣1<x<3时,ax2+bx+c<0,而x=﹣1或x=3时,ax2+bx+c=0,所以④错误;
设抛物线的解析式为y=a(x+1)(x﹣3)=ax2﹣2ax﹣3a,对称轴x=1交x轴与E点,如图,当△ABD是等腰直角三角形,则DE=![]() AB,即|
AB,即|![]() |=
|=![]() ×4,∴a=
×4,∴a=![]() ,所以⑤正确.
,所以⑤正确.
故答案为:①⑤.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,形如
 的点涂上红色(其中
的点涂上红色(其中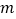 、
、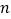 为整数),称为红点,其余不涂色,那么抛物线
为整数),称为红点,其余不涂色,那么抛物线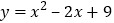 上有( )个红点.
上有( )个红点.A.
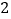 个 B.
个 B. 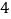 个 C.
个 C. 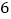 个 D. 无数个
个 D. 无数个 -
科目: 来源: 题型:
查看答案和解析>>【题目】有下列六个命题:①相等的角是对顶角;②两直线平行,同位角相等;③若一个三角形的两个内角分别为
 和
和 ,则这个三角形是直角三角形;④全等三角形的对应角相等。其中逆命题是假命题的个数有( )
,则这个三角形是直角三角形;④全等三角形的对应角相等。其中逆命题是假命题的个数有( )A.0个B.1个C.2个D.3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,抛物线
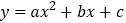 的部分图象如图,则下列说法:①对称轴是直线
的部分图象如图,则下列说法:①对称轴是直线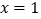 ;②当
;②当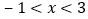 时,
时, ;③
;③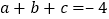 ;④方程
;④方程 无实数根,其中正确的有________.
无实数根,其中正确的有________.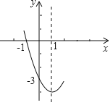
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有长为
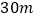 的篱笆,一面利用墙(墙的最大可用长度为
的篱笆,一面利用墙(墙的最大可用长度为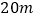 ),围成中间隔有一道篱笆(平行于
),围成中间隔有一道篱笆(平行于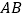 )的矩形花圃
)的矩形花圃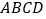 .设花圃的一边
.设花圃的一边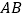 为
为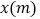 .
.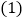 则
则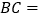 ________(用含
________(用含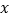 的代数式表示),矩形
的代数式表示),矩形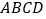 的面积
的面积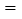 ________(用含
________(用含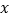 的代数式表示);
的代数式表示);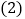 如果要围成面积为
如果要围成面积为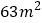 的花圃,
的花圃,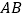 的长是多少?
的长是多少?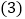 将
将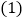 中表示矩形
中表示矩形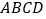 的面积的代数式通过配方,问:当
的面积的代数式通过配方,问:当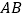 等于多少时,能够使矩形花圃
等于多少时,能够使矩形花圃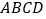 面积最大,最大的面积为多少?
面积最大,最大的面积为多少?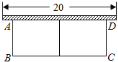
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,对称轴为
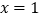 的抛物线
的抛物线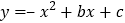 与
与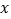 轴交于
轴交于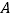 、
、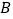 两点,与
两点,与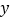 轴交于
轴交于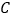 点,其中
点,其中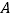 点坐标为
点坐标为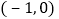 设抛物线的顶点为
设抛物线的顶点为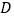 .
.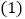 求抛物线的解析式及顶点坐标;
求抛物线的解析式及顶点坐标;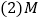 为
为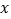 轴上的一点,当
轴上的一点,当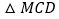 的周长最小时,求点
的周长最小时,求点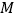 的坐标及
的坐标及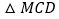 的周长.
的周长.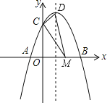
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售一批衬衫,平均每天可售出
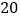 件,每件盈利
件,每件盈利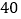 元.为了扩大销售,增加盈利,商场决定采取适当的降价措施.经调查发现,在一定范围内,衬衫的单价每下降
元.为了扩大销售,增加盈利,商场决定采取适当的降价措施.经调查发现,在一定范围内,衬衫的单价每下降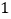 元,商场平均每天可多售出
元,商场平均每天可多售出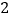 件.
件.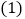 如果商场通过销售这批衬衫每天获利
如果商场通过销售这批衬衫每天获利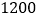 元,那么衬衫的单价应下降多少元?
元,那么衬衫的单价应下降多少元? 当每件衬衫的单价下降多少元时,每天通过销售衬衫获得的利润最大?最大利润为多少元?
当每件衬衫的单价下降多少元时,每天通过销售衬衫获得的利润最大?最大利润为多少元?
相关试题

