【题目】小明在课外学习时遇到这样一个问题:
定义:如果二次函数![]() 是常数与
是常数与![]() 是常数)满足
是常数)满足![]() ,则称这两个函数互为“旋转函数”.
,则称这两个函数互为“旋转函数”.
求函数![]() 的 “旋转函数”.
的 “旋转函数”.
小明是这样思考的:由![]() 函数可知a1=-1,b1=3,c1=-3,根据a1+a2=0,b1=b2,c1+c2=0求出a2,b2,c2,就能确定这个函数的“旋转函数”.
函数可知a1=-1,b1=3,c1=-3,根据a1+a2=0,b1=b2,c1+c2=0求出a2,b2,c2,就能确定这个函数的“旋转函数”.
请参考小明的方法解决下面的问题:
(1)写出函数![]() 的“旋转函数”;
的“旋转函数”;
(2)若函数![]() 与
与![]() 互为“旋转函数”,求(m+n)2017的值;
互为“旋转函数”,求(m+n)2017的值;
(3)已知函数![]() 的图象与
的图象与![]() 轴交于A、B两点,与y轴交于点C,点A、B、C关于原点的对称点分别是A1、B1、C1,试证明经过点A1、B1、C1的二次函数与函数
轴交于A、B两点,与y轴交于点C,点A、B、C关于原点的对称点分别是A1、B1、C1,试证明经过点A1、B1、C1的二次函数与函数![]() 互为“旋转函数”.
互为“旋转函数”.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)证明见解析
;(3)证明见解析
【解析】解:(1)由![]() 函数可知,
函数可知, ![]()
∵![]() ,
,
∴![]()
∴函数![]() 的“旋转函数”是
的“旋转函数”是![]()
(2)函数![]() 与
与![]() 互为“旋转函数”
互为“旋转函数”
∴![]()
![]()
∴![]()
(3)数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]()
∴![]()
∴![]()
得过点![]() 的二次函数是
的二次函数是![]()
∵![]() =
=![]()
∴![]()
∴经过点![]() 的二次函数与函数
的二次函数与函数![]() 互为“旋转函数”.
互为“旋转函数”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠A为锐角,且tan35°cotA=1,则∠A=________度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=mx+n与反比例函数
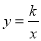 交于A、B两点,点A在点B的左边,与x轴、y轴分别交于点C、点D,AE⊥x轴于E,BF⊥y轴于F
交于A、B两点,点A在点B的左边,与x轴、y轴分别交于点C、点D,AE⊥x轴于E,BF⊥y轴于F(1)直接写出m、n、k的正负性
(2) 若m=1,n=3,k=4,求直线EF的解析式
(3)写出AC、BD的数量关系,并证明

-
科目: 来源: 题型:
查看答案和解析>>【题目】在括号内填入每步运算的依据.
解:(﹣8)+(﹣5)+8
=(﹣8)+8+(﹣5)
=[(﹣8)+8]+(﹣5)
=0+(﹣5)
=(﹣5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若△ABC∽△DEF,它们的面积比为4:1,则△ABC与△DEF的相似比为( )
A. 2:1B. 1:2
C. 4:1D. 1:4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=0是方程x2+bx+b﹣3=0的一个根,那么此方程的另一个根为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】把多项式﹣x3﹣7x2y+y3﹣4xy2重新排列
(1)按x的升幂排列;
(2)按y的升幂排列.
相关试题

