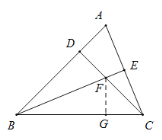
【题目】在△ABC中,BA=BC,BE平分∠ABC,CD⊥BD,且CD=BD.
(1)求证:BF=AC;
(2)若AD=![]() ,求CF的长.
,求CF的长.

参考答案:
【答案】(1)证明见解析;(2)2.
【解析】
(1)已知AB=AC,BE平分∠ABC,根据等腰三角形三线合一的性质可得BE⊥AC,所以∠ABE+∠A=90°,再由∠ACD+∠A=90°,根据同角的余角相等可得∠ABE=∠ACD,利用ASA判定△BDF≌△CDA,根据全等三角形的性质即可证得BF=AC;(2)如图,过点F作FG⊥BC于点G, 根据角平分线的性质定理可得FD=FG,由△BDF≌△CDA即可得DF=AD=![]() =FG,已知CD⊥BD,CD=BD,根据等腰三角形的性质可得∠DCB=45°,即可求得CF=2 .
=FG,已知CD⊥BD,CD=BD,根据等腰三角形的性质可得∠DCB=45°,即可求得CF=2 .
(1)∵AB=AC,BE平分∠ABC
∴BE⊥AC
∴∠ABE+∠A=90°
∵CD⊥AB
∴∠ACD+∠A=90°
∴∠ABE=∠ACD
∵∠ADC=∠BDF=90°,BD=CD
∴△BDF≌△CDA(ASA)
∴BF=AC
(2)如图,过点F作FG⊥BC于点G, 则FD=FG .
∵△BDF≌△CDA
∴DF=AD=![]() =FG
=FG
∵CD⊥BD,CD=BD
∴∠DCB=45°
∴CF=2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x,y的方程组

(1)请直接写出方程
 的所有正整数解
的所有正整数解(2)若方程组的解满足x+y=0,求m的值
(3)无论实数m取何值,方程x-2y+mx+5=0总有一个固定的解,请直接写出这个解?
(4)若方程组的解中x恰为整数,m也为整数,求m的值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了响应“中小学生每天锻炼1小时”的号召,某校开展了形式多样的“阳光体育”活动,小明对某班同学参加锻炼的情况进行了调查与统计,并绘制了下面的图1与图2.根据你对图1与图2的理解,回答下列问题:
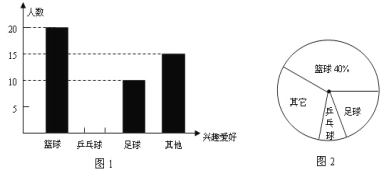
(1)小明调查的这个班级有多少名学生,参加足球锻炼的学生人数所占的百分比是多少?
(2)请你将图1中“乒乓球”部分补充完整.
(3)求出扇形统计图中表示“足球”的扇形的圆心角的度数.
(4)若这个学校共有1200名学生,估计参加乒乓球活动的学生有多少名学生?
-
科目: 来源: 题型:
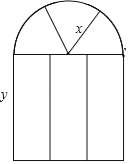
查看答案和解析>>【题目】某窗户的形状如图所示(图中长度单位:cm),其中上部是半径为xcm的半圆形,下部是宽为ycm的长方形.
(1)用含x,y的式子表示窗户的面积S;
(2)当x=40,y=120时,求窗户的面积S.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于点Q.
(1)如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;
(2)如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.

-
科目: 来源: 题型:
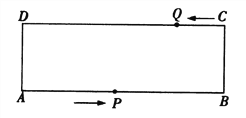
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=24 cm, BC=8 cm,点P从点A开始沿折线A-B-C-D以4 cm/s的速度移动,点Q从点C开始沿CD边以2 cm/s的速度移动,如果点P,Q分别从点A,C同时出发,当其中一点到达点D时,另一点也随之停止运动,设运动时间为ts.当t为何值时,四边形QPBC为矩形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】取一张正方形的纸片进行折叠,具体操作过程如下:
第一步:如图1,先把正方形ABCD对折,折痕为MN.
第二步:点G在线段 MD上,将△GCD沿GC翻折,点D恰好落在MN上,记为点P,连接BP.
(1)判断△PBC的形状,并说明理由;
(2)作点C关于直线AP的对称点C′,连接PC′、DC′.
①在图2中补全图形,并求出∠APC′的度数;
②猜想∠PC′D的度数,并加以证明;(温馨提示:当你遇到困难时,不妨连接AC′、CC′,研究图形中特殊的三角形)
相关试题

