【题目】为了响应“中小学生每天锻炼1小时”的号召,某校开展了形式多样的“阳光体育”活动,小明对某班同学参加锻炼的情况进行了调查与统计,并绘制了下面的图1与图2.根据你对图1与图2的理解,回答下列问题:
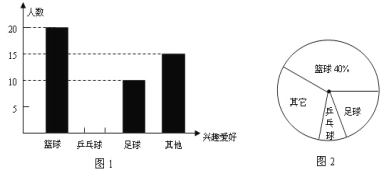
(1)小明调查的这个班级有多少名学生,参加足球锻炼的学生人数所占的百分比是多少?
(2)请你将图1中“乒乓球”部分补充完整.
(3)求出扇形统计图中表示“足球”的扇形的圆心角的度数.
(4)若这个学校共有1200名学生,估计参加乒乓球活动的学生有多少名学生?
参考答案:
【答案】(1)小明调查的这个班级有50名学生,参加足球锻炼的学生人数所占的百分比是20%;(2)见解析;(3)扇形统计图中表示“足球”的扇形的圆心角的度数为72°;(4)参加乒乓球活动的学生有120名学生
【解析】
(1)利用参加篮球锻炼的学生人数除以其所占该班总人数的百分比即可求出该班总人数,然后利用参加足球锻炼的学生人数除以该班总人数即可求出所占的百分比;
(2)利用该班总人数减去“篮球”、“足球”和“其它”的人数即可求出“乒乓球”的人数,然后补全条形统计图即可;
(3)利用参加足球锻炼的学生人数所占的百分比再乘360°即可求出结论;
(4)求出参加乒乓球活动的学生所占的百分比再乘1200即可求出结论.
解:(1)该班总人数为20÷40%=50(名)
参加足球锻炼的学生人数所占的百分比是10÷50×100%=20%
答:小明调查的这个班级有50名学生,参加足球锻炼的学生人数所占的百分比是20%.
(2)“乒乓球”的人数为50-20-10-15=5(名)
补全条形统计图如下
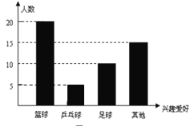
(3)表示“足球”的扇形的圆心角的度数为20%×360°=72°
答:扇形统计图中表示“足球”的扇形的圆心角的度数为72°.
(4)5÷50×1200=120(名)
答:参加乒乓球活动的学生有120名学生.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着人们环保意识的增强,“低碳生活”成为人们提倡的生活方式,黄先生要从某地到福州,若乘飞机需要3小时,乘汽车需要9小时.这两种交通工具每小时排放的二氧化碳总量为70千克,已知飞机每小时二氧化碳的排放量比汽车多44千克,黄先生若乘汽车去福州,那么他此行与乘飞机相比减少二氧化碳排放量多少千克?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在⊙O 中,P是⊙O内一点,过点P最短和最长的弦分别为6和10,则经过点P且长度为整数的的弦共有( )条。
A.5
B.8
C.10
D.无数条 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x,y的方程组

(1)请直接写出方程
 的所有正整数解
的所有正整数解(2)若方程组的解满足x+y=0,求m的值
(3)无论实数m取何值,方程x-2y+mx+5=0总有一个固定的解,请直接写出这个解?
(4)若方程组的解中x恰为整数,m也为整数,求m的值。
-
科目: 来源: 题型:
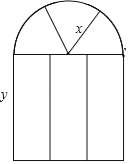
查看答案和解析>>【题目】某窗户的形状如图所示(图中长度单位:cm),其中上部是半径为xcm的半圆形,下部是宽为ycm的长方形.
(1)用含x,y的式子表示窗户的面积S;
(2)当x=40,y=120时,求窗户的面积S.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,BA=BC,BE平分∠ABC,CD⊥BD,且CD=BD.
(1)求证:BF=AC;
(2)若AD=
 ,求CF的长.
,求CF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于点Q.
(1)如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;
(2)如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.

相关试题

