【题目】取一张正方形的纸片进行折叠,具体操作过程如下:
第一步:如图1,先把正方形ABCD对折,折痕为MN.
第二步:点G在线段 MD上,将△GCD沿GC翻折,点D恰好落在MN上,记为点P,连接BP.
(1)判断△PBC的形状,并说明理由;
(2)作点C关于直线AP的对称点C′,连接PC′、DC′.
①在图2中补全图形,并求出∠APC′的度数;
②猜想∠PC′D的度数,并加以证明;(温馨提示:当你遇到困难时,不妨连接AC′、CC′,研究图形中特殊的三角形)
参考答案:
【答案】
(1)解:△PBC是等边三角形,理由如下:
∵四边形ABCD是正方形,
∴AB=BC=CD,∠ABC=90°,
由折叠的性质得:BN=NC= ![]() BC=
BC= ![]() PC,MN⊥BC,
PC,MN⊥BC,
∴PB=PC,∠PNC=90°,
在Rt△PNC中,sin∠NPC= ![]() =
= ![]() ,
,
∴∠NPC=30°,
∴∠PCB=60°,
∴△PBC是等边三角形
(2)解:①补全图形如图2所示:
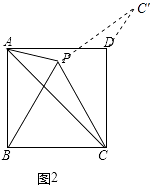
由①得:∠PCB=∠PBC=∠BPC=60°,PB=PC=BC,
∵∠ABC=90°,
∴∠ABP=90°﹣60°=30°,
∵AB=BC,
∴AB=PB,
∴∠BAP=∠BPA= ![]() (180°﹣30°)=75°,
(180°﹣30°)=75°,
∴∠APC=∠BPA+∠BPC=75°+60°=135°,
∵C关于直线AP的对称点为C′,
∴∠APC'=∠APC=135°;
②连接AC',CC',如图3所示:
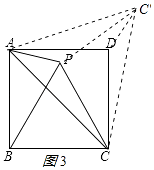
由对称的性质得:AC=AC',∠CAP=∠C'AP=30°,
∴∠CAC'=60°,
∴△CAC'是等边三角形,
∴AC'=CC',∠AC'C=60°,
在△AC'D和△CC'D中, 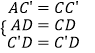 ,
,
∴△AC'D≌△CC'D(SSS),
∴∠AC'D=∠CC'D= ![]() ∠AC'C=30°,
∠AC'C=30°,
∵∠AC'P=∠ACP=15°,
∴∠PC'D=15°.
【解析】(1)由正方形的性质得出AB=BC=CD,∠ABC=90°,由折叠的性质得:BN=NC= ![]() BC=
BC= ![]() PC,MN⊥BC,得出PB=PC,∠PNC=90°,在Rt△PNC中,由三角函数得出sin∠NPC=
PC,MN⊥BC,得出PB=PC,∠PNC=90°,在Rt△PNC中,由三角函数得出sin∠NPC= ![]() =
= ![]() ,求出∠NPC=30°,得出∠PCB=60°,即可得出结论;(2)①根据题意补全图形,由①得:∠PCB=∠PBC=∠BPC=60°,PB=PC=BC,由等腰三角形的性质和三角形内角和定理得出∠BAP=∠BPA=75°,求出∠APC=∠BPA+∠BPC=135°,再由得出的性质得出∠APC'=∠APC=135°;②由对称的性质得:AC=AC',∠CAP=∠C'AP=30°,证出△CAC'是等边三角形,得出AC'=CC',∠AC'C=60°,由SSS证明△AC'D≌△CC'D,得出∠AC'D=∠CC'D=
,求出∠NPC=30°,得出∠PCB=60°,即可得出结论;(2)①根据题意补全图形,由①得:∠PCB=∠PBC=∠BPC=60°,PB=PC=BC,由等腰三角形的性质和三角形内角和定理得出∠BAP=∠BPA=75°,求出∠APC=∠BPA+∠BPC=135°,再由得出的性质得出∠APC'=∠APC=135°;②由对称的性质得:AC=AC',∠CAP=∠C'AP=30°,证出△CAC'是等边三角形,得出AC'=CC',∠AC'C=60°,由SSS证明△AC'D≌△CC'D,得出∠AC'D=∠CC'D= ![]() ∠AC'C=30°,由∠AC'P=∠ACP=15°,即可得出∠PC'D=15°.
∠AC'C=30°,由∠AC'P=∠ACP=15°,即可得出∠PC'D=15°.
【考点精析】本题主要考查了全等三角形的性质和正方形的性质的相关知识点,需要掌握全等三角形的对应边相等; 全等三角形的对应角相等;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,BA=BC,BE平分∠ABC,CD⊥BD,且CD=BD.
(1)求证:BF=AC;
(2)若AD=
 ,求CF的长.
,求CF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于点Q.
(1)如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;
(2)如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.

-
科目: 来源: 题型:
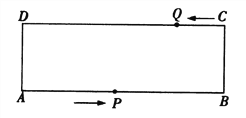
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=24 cm, BC=8 cm,点P从点A开始沿折线A-B-C-D以4 cm/s的速度移动,点Q从点C开始沿CD边以2 cm/s的速度移动,如果点P,Q分别从点A,C同时出发,当其中一点到达点D时,另一点也随之停止运动,设运动时间为ts.当t为何值时,四边形QPBC为矩形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图所示,O为数轴的原点,A,B分别为数轴上的两点,A点对应的数为﹣30,B点对应的数为100.
(1)A、B的中点C对应的数是 ;
(2)若点D数轴上A、B之间的点,D到B的距离是D到A的距离的3倍,求D对应的数.(提示:数轴上右边的点对应的数减去左边对应的数等于这两点间的距离);
(3)若P点和Q点是数轴上的两个动点,当P点从B点出发,以6个单位长度/秒的速度向左运动时,Q点也从A点出发,以4个单位长度/秒的速度向右运动,设两点在数轴上的E点处相遇,那么E点对应的数是多少?

-
科目: 来源: 题型:
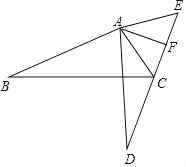
查看答案和解析>>【题目】如图,∠BAD=∠CAE,AB=AD,AC=AE.且E,F,C,D在同一直线上.
(1)求证:△ABC≌△ADE;
(2)若∠B=30°,∠BAC=100°,点F是CE的中点,连结AF,求∠FAE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,这是某市部分简图,为了确定各建筑物的位置:

(1)请你以火车站为原点建立平面直角坐标系,若以小方格的边长为单位长度,写出市场的坐标为_______;超市的坐标为_____________.
(2)请将体育场为A、宾馆为C和火车站为B看作三点用线段连起来,得△ABC,然后将△ABC向下平移4个单位长度,画出平移后的
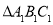 ,写出
,写出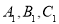 的坐标.
的坐标.(3)求出
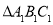 的面积.
的面积.
相关试题

