搜索
【题目】将抛物线y=x2﹣4x+1向左平移2个单位，再向上平移3个单位所得抛物线解析式为 ．
参考答案：
【答案】y=x2
【解析】解：∵y=x2﹣4x+1， =x2﹣4x+4﹣4+1，
=（x﹣2）2﹣3，
∴原抛物线顶点坐标为（2，﹣3），
∵向左平移2个单位，再向上平移3个单位，
∴平移后的抛物线顶点坐标为（0，0），
∴所得抛物线解析式为y=x2 ．
所以答案是：y=x2 ．
【考点精析】本题主要考查了二次函数图象的平移的相关知识点，需要掌握平移步骤：（1）配方 y=a(x-h)2+k，确定顶点（h,k）（2）对x轴左加右减；对y轴上加下减才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】解答
（1）如图（1），已知：在△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D，E．
证明：DE=BD+CE．
（2）如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D，A，E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意锐角或钝角．请问结论DE=BD+CE是否成立？如成立，请你给出证明；若不成立，请说明理由．
（3）拓展与应用：如图（3），D，E是D，A，E三点所在直线m上的两动点（D，A，E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD，CE，若∠BDA=∠AEC=∠BAC，试判断△DEF的形状．
-
科目： 来源： 题型：
查看答案和解析>>【题目】枣庄乐园设置了一个秋千场所，如图所，秋千拉绳OB的长为3m，静止时，踏板到地面距离BD的长为0.6m（踏板厚度忽略不计）．为安全起见，乐园管理处规定：儿童的“安全高度”为hm，成人的“安全高度”为2m（计算结果精确到0.1m）
（1）当摆绳OA与OB成45°夹角时，恰为儿童的安全高度，求h的长；
（2）某成人在玩秋千时，摆绳OC与OB的最大夹角为55°，问此人是否安全？（参考数据：
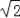≈1.41，sin55°≈0.82，cos55°≈0.57，tan55°≈1.43）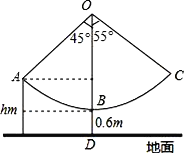
-
科目： 来源： 题型：
查看答案和解析>>【题目】直线y＝
x＋4与x轴、y轴分别交于点A和点B，点C，D分别为线段AB，OB的中点，点P为OA上一动点，PC＋PD值最小时点P的坐标为.
A. (－3，0) B. (－6，0) C. (－
，0) D. (－
，0) -
科目： 来源： 题型：
查看答案和解析>>【题目】下列计算正确的是（ ）
A.a+a=a2
B.6a3﹣5a2=a
C.3a2+2a3=5a5
D.3a2b﹣4ba2=﹣a2b -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线l是一条河，A，B两地相距5km，A，B两地到l的距离分别为3km、6km，欲在l上的某点M处修建一个水泵站，向A，B两地供水，现有如下四种铺设方案，图中实线表示铺设的管道，则铺设的管道最短的是（ ）
A.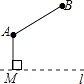
B.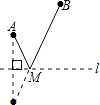
C.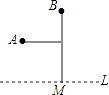
D.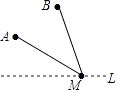
-
科目： 来源： 题型：
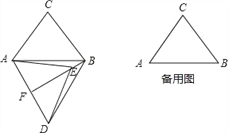
查看答案和解析>>【题目】在△ABC中,AB=6,AC=BC=5,将△ABC绕点A按顺时针方向旋转,得到△ADE,旋转角为α（0°＜α＜180°）,点B的对应点为点D,点C的对应点为点E,连接BD，BE．
（1）如图,当α=60°时,延长BE交AD于点F．
①求证：△ABD是等边三角形；
②求证：BF⊥AD，AF=DF；
③请直接写出BE的长；
（2）在旋转过程中,过点D作DG垂直于直线AB,垂足为点G,连接CE,当∠DAG=∠ACB,且线段DG与线段AE无公共点时,请直接写出BE+CE的值．
相关试题
