【题目】制作一种产品,需先将材料加热达到60℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(分钟).据了解,设该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加工前的温度为15℃,加热5分钟后温度达到60℃.

(1)、求出将材料加热时,y与x的函数关系式;
(2)、求出停止加热进行操作时,y与x的函数关系式;
(3)、根据工艺要求,当材料的温度低于15℃时,须停止操作,那么操作时间是多少?
参考答案:
【答案】(1)、y=9x+15;(2)、y=![]() ;(3)、15分钟
;(3)、15分钟
【解析】
试题分析:(1)、设一次函数解析式为y=kx+b,将(0,15)和(5,60)代入一次函数解析式求出k和b的值;(2)、设反比例函数的解析式为y=![]() ,将(5,60)代入求出函数解析式;(3)、将y=15代入反比例函数解析式求出x的值,然后再减去5分钟就是操作的时间.
,将(5,60)代入求出函数解析式;(3)、将y=15代入反比例函数解析式求出x的值,然后再减去5分钟就是操作的时间.
试题解析:(1)、设函数解析式为y=kx+b 将(0,15)和(5,60)代入函数解析式可得:![]()
解得:![]() ∴一次函数的解析式为:y=9x+15
∴一次函数的解析式为:y=9x+15
、设反比例函数的解析式为:y=![]() 将(5,60)代入得:k=300 则反比例函数解析式为:y=
将(5,60)代入得:k=300 则反比例函数解析式为:y=![]() .
.
、将y=15代入反比例函数解析式可得:x=20 20-5=15(分钟)
即操作时间为15分钟.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2+2x+m=0的有两个相等的实数根,则m为( )
A.2
B.﹣2
C.1
D.﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】细观察,找规律 下列各图中的MA1与NAn平行.

(1)图①中的∠A1+∠A2=度, 图②中的∠A1+∠A2+∠A3=度,
图③中的∠A1+∠A2+∠A3+∠A4=度,
图④中的∠A1+∠A2+∠A3+∠A4+∠A5=度,
…,
第⑩个图中的∠A1+∠A2+∠A3+…+∠A11=度
(2)第n个图中的∠A1+∠A2+∠A3+…+∠An+1=
(3)请你证明图②的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠1=∠2.求证:∠3+∠4=180° 证明:∵∠1=∠2(已知)
∴a∥b()
∴∠3+∠5=180°(两直线平行,同旁内角互补)
又∵∠4=∠5()
∴∠3+∠4=180°(等量代换)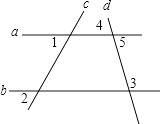
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. 3a﹣a=3B. (a2)3=a6C. 3a+2a=2a2D. a2﹣a2=a4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一次实践活动中,小强从A地出发,沿北偏东60°的方向行进3
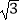 千米到达B地,然后再沿北偏西30°方向行进了3千米到达目的地C.
千米到达B地,然后再沿北偏西30°方向行进了3千米到达目的地C. 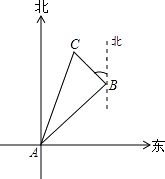
(1)求A、C两地之间的距离;
(2)试确定目的地C在点A的什么方向? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆的半径为r,圆心到直线a的距离为d,d和r分别是方程x2﹣7x+10=0的两根,则直线a与圆的位置关系是( )
A. 相交B. 相切C. 相交或相离D. 相离
相关试题

