【题目】已知抛物线y=﹣x2+bx+c与x轴交于点A(1,0),B(3,0),与y轴交于点C. 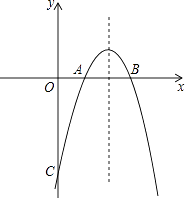
(1)求抛物线的解析式;
(2)设点P在该抛物线上滑动,则满足S△PAB=1的点P有几个?求出所有点P的坐标;
(3)在该抛物线的对称轴上存在点M,使得△MAC的周长最小,求出这个点M的坐标.
参考答案:
【答案】
(1)解:将点A(1,0)、B(3,0)代入y=﹣x2+bx+c中,
得: ![]() ,解得:
,解得: ![]() ,
,
∴该抛物线的解析式为y=﹣x2+4x﹣3
(2)解:设点P的坐标为(x,y).
∵AB=2,S△PAB= ![]() AB|y|=1,
AB|y|=1,
∴y=±1.
当y=1时,有1=﹣x2+4x﹣3,即x2﹣4x+4=(x﹣2)2=0,
解得:x1=x2=2;
当y=﹣1时,有﹣1=﹣x2+4x﹣3,即x2﹣4x+2=0,
解得:x3=2﹣ ![]() ,x4=2+
,x4=2+ ![]() .
.
∴满足条件的点P有三个坐标分别为(2,1),(2+ ![]() ,﹣1),(2﹣
,﹣1),(2﹣ ![]() ,﹣1)
,﹣1)
(3)解:假设存在.
过点C作抛物线的对称轴的对称点C′,连接AC′交抛物线对称轴于点M,连接MC,任取抛物线对称轴上除M外的任意一点N,连接NA,NC、NC′,如图所示.
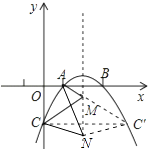
∵NA+NC=NA+NC′>AC′=MA+MC′=MA+MC,
∴当点A、M、C′三点共线时,△MAC的周长最小.
∵抛物线的解析式为y=﹣x2+4x﹣3,
∴点C的坐标为(0,﹣3),抛物线的对称轴为x=﹣ ![]() =2,
=2,
∴C′(4,﹣3).
设直线AC′的解析式为y=mx+n,
∵点A(1,0)、C′(4,﹣3)在直线AC′上,
∴ ![]() ,解得:
,解得: ![]() ,
,
∴直线AC′的解析式为y=﹣x+1.
联立直线AC′的解析式和抛物线的对称轴成方程组: ![]() ,
,
解得: ![]() .
.
∴直线AC′与对称轴x=2的交点为(2,﹣1),即M(2,﹣1),
∴存在点M(2,﹣1),可使△AMC的周长最小
【解析】(1)结合点A、B的坐标,利用待定系数法即可求出抛物线的解析式;(2)设点P的坐标为(x,y).结合三角形的面积公式求出y=±1,将其代入抛物线解析式中求出x值,由此即可得出结论;(3)假设存在,过点C作抛物线的对称轴的对称点C′,连接AC′交抛物线对称轴于点M,连接MC,任取抛物线对称轴上除M外的任意一点N,连接NA,NC、NC′,利用三角形两边之和大于第三边得出点A、M、C′三点共线时,△MAC的周长最小.由抛物线的解析式找出点C的坐标以及抛物线的对称轴,利用对称的性质找出点C′的坐标,结合点A、C′的坐标利用待定系数法求出直线AC′的解析式,再联立直线AC′的解析式与抛物线的对称轴成方程组,解方程组即可求出点M的坐标.
【考点精析】根据题目的已知条件,利用抛物线与坐标轴的交点的相关知识可以得到问题的答案,需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(﹣2,2),B(﹣3,﹣2)

(1)若点C与点A关于原点O对称,则点C的坐标为 ;
(2)将点A向右平移5个单位得到点D,则点D的坐标为 ;
(3)由点A,B,C,D组成的四边形ABCD内(不包括边界)任取一个横、纵坐标均为整数的点,求所取的点横、纵坐标之和恰好为零的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,直径AB与弦CD相交于点P,∠CAB=40°,∠APD=65°.

(1)求∠B的大小;
(2)已知圆心0到BD的距离为3,求AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象回答下列问题.
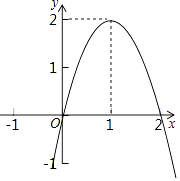
(1)写出方程ax2+bx+c=0的根;
(2)写出不等式ax2+bx+c<0的解集;
(3)若方程ax2+bx+c=k无实数根,写出k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】课堂上学习了勾股定理后,知道“勾三、股四、弦五”.王老师给出一组数让学生观察:3、4、5;5、12、13;7、24、25;9、40、41;…,学生发现这些勾股 数的勾都是奇数,且从 3 起就没有间断过,于是王老师提出以下问题让学生解决.
(1)请你根据上述的规律写出下一组勾股数:11、________、________;
(2)若第一个数用字母a(a为奇数,且a≥3)表示,那么后两个数用含a的代数式分别怎么表示?小明发现每组第二个数有这样的规律4=
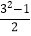 ,12=
,12=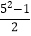 ,24=
,24=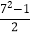 ……,于是他很快表示了第二数为
……,于是他很快表示了第二数为  ,则用含a的代数式表示第三个数为________;
,则用含a的代数式表示第三个数为________;(3)用所学知识证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣(2k+1)x+k2+k=0.
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB,AC的长是这个方程的两个实数根.第三边BC的长为5,当△ABC是等腰三角形时,求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】“低碳环保,绿色出行”的概念得到广大群众的接受,越来越多的人喜欢选择骑自行车作为出行工具.小军和爸爸同时骑车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆.小军始终以同一速度骑行,两人骑行的路程为y(米)与时间x(分钟)的关系如图.请结合图象,解答下列问题:
(1)填空:a=________;b=________;m=________.
(2)若小军的速度是 120 米/分,求小军第二次与爸爸相遇时距图书馆的距离.
(3)在(2)的条件下,爸爸自第二次出发后,骑行一段时间后与小军相距100 米,此时 小军骑行的时间为________分钟.

相关试题

