【题目】“垃圾不落地,商南更美丽”。某中学为了了解七年级学生对这个一倡议的落实情况,学校安排政教处在七年级学生中随机抽取了部分学生,并针对学生“是否随手丢垃圾”这一情况进行了问卷调查,将这一情况分为:![]() ——从不随手丢垃圾;
——从不随手丢垃圾;![]() ——偶尔随手丢垃圾;
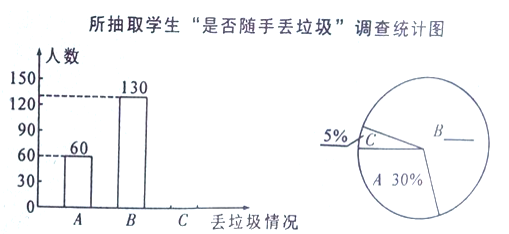
——偶尔随手丢垃圾;![]() ——经常随手丢垃圾三项。要求每位被调查的学生必须从以上三项中选一项且只能选一项。现将调查结果绘制成以下两幅不完整的统计图。请你根据以上信息,解答下列问题:
——经常随手丢垃圾三项。要求每位被调查的学生必须从以上三项中选一项且只能选一项。现将调查结果绘制成以下两幅不完整的统计图。请你根据以上信息,解答下列问题:
(1)补全条形统计图和扇形统计图;
(2)图中“偶尔随手丢垃圾”所在扇形的圆心角为______________;
(3)若该校七年级共有1500名学生,请你估计该年级学生中“经常随手丢垃圾”的学生约有多少人?谈谈你的看法?
参考答案:
【答案】(1)见解析;(2)234°;(3)75人,见解析.
【解析】
(1)根据A情况的人数及其所占百分比求得总人数,用总人数减去A、B人数求得C情况的人数,再用B情况人数除以总人数可得其百分比;
(2)根据统计图中的数据可以求得扇形统计图中B所在扇形的圆心角度数;
(3)总人数乘以样本中C情况的百分比可得.
解:(1)∵被调查的总人数为60÷30%=200人,
∴C情况的人数为200-(60+130)=10人,B情况人数所占比例为
![]() ×100%=65%,
×100%=65%,
补全图形如下:
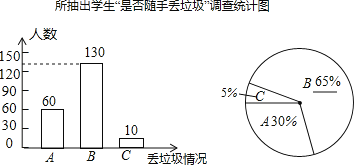 ;
;
(2)由(1)知B情况人数所占比例为65%,所以圆心角65%×![]() =
=![]() ;
;
(3)∵“经常随手丢垃圾”的学生所占比例为5%,
∴1500×5%=75(人),
答:估计该年级学生中“经常随手丢垃圾”的学生约有75人,就该年级经常随手丢垃圾的学生人数看出仍需要加强公共卫生教育、宣传和监督.
-
科目: 来源: 题型:
查看答案和解析>>【题目】开学初,小聪去某文具商店购买学习用品的数据如下表(因污损导致部分数据无法识别):
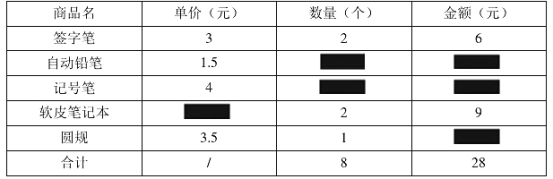
仔细观察表格中数据之间的关系,解决下列问题:
(1)这家文具商店软面笔记本的单价是________元/本,小聪购买圆规共花费______元;
(2)小聪购买了自动铅笔、记号笔各几支?
(3)若小明也在同一家文具店购买了软面笔记本和自动铅笔两种文具,已知他恰好花费12元,请你对小明购买的软面笔记本和自动铅笔数量的可能性进行分析。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点。
(1)画出
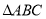 向下平移2个单位,再向右平移3个单位后得到的
向下平移2个单位,再向右平移3个单位后得到的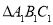 ;
;(2)图中
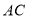 与
与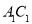 的关系是:____________________;
的关系是:____________________;(3)图中
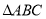 的面积是___________________________。
的面积是___________________________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.
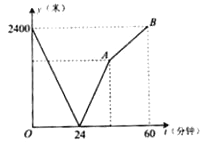
(1)根据图象信息,当t=________分钟时甲乙两人相遇,甲的速度为________米/分钟;
(2)求出线段AB所表示的函数表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
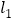 的解析表达式为:y=-3x+3,且
的解析表达式为:y=-3x+3,且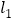 与x轴交于点D,直线
与x轴交于点D,直线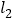 经过点A,B,直线
经过点A,B,直线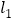 ,
,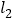 交于点C.
交于点C.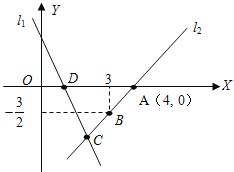
(1)求点D的坐标;
(2)求直线
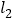 的解析表达式;
的解析表达式;(3)求△ADC的面积;
(4)在直线
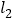 上存在异于点C的另一点P,使得△ADP的面积是△ADC面积的2倍,请直接写出点P的坐标.
上存在异于点C的另一点P,使得△ADP的面积是△ADC面积的2倍,请直接写出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明购买A,B两种商品,每次购买同一种商品的单价相同,具体信息如下表:
次数
购买数量(件

购买总费用(元

A
B
第一次
2
1
55
第二次
1
3
65
根据以上信息解答下列问题:
(1)求A,B两种商品的单价;
(2)若第三次购买这两种商品共12件,且A种商品的数量不少于B种商品数量的2倍,请设计出最省钱的购买方案,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(问题情境)
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
(探究展示)
(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
(拓展延伸)
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.

相关试题

