【题目】如图,抛物线y=![]() x2+bx+c经过点B(3,0)、C(0,﹣2),直线L:y=﹣
x2+bx+c经过点B(3,0)、C(0,﹣2),直线L:y=﹣![]() x﹣
x﹣![]() 交y轴于点E,且与抛物线交于A、D两点,P为抛物线上一动点(不与A、D重合).
交y轴于点E,且与抛物线交于A、D两点,P为抛物线上一动点(不与A、D重合).
(1)求抛物线的解析式;
(2)当点P在直线L下方时,过点P作PN∥y轴交L于点N,求PN的最大值.
(3)当点P在直线L下方时,过点P作PM∥x轴交L于点M,求PM的最大值.

参考答案:
【答案】(1)抛物线的解析式为:y=![]() x2﹣
x2﹣![]() x﹣2;(2)PN的最大值是
x﹣2;(2)PN的最大值是![]() ;(3)PM的最大值是
;(3)PM的最大值是![]() .
.
【解析】试题分析:(1)把B(3,0),C(0,-2)代入y=![]() x2+bx+c解方程组即可得到结论;
x2+bx+c解方程组即可得到结论;
(2)设P(m, ![]() m2-
m2-![]() m-2),得到N(m,-
m-2),得到N(m,-![]() m-
m-![]() ),根据二次函数的性质即可得到结论;
),根据二次函数的性质即可得到结论;
(3)设P(m, ![]() m2-
m2-![]() m-2),得到M(-m2+2m+2,
m-2),得到M(-m2+2m+2, ![]() m2-
m2-![]() m-2),根据二次函数的性质即可得到结论.
m-2),根据二次函数的性质即可得到结论.
试题解析:(1)把B(3,0),C(0,﹣2)代入y=![]() x2+bx+c,
x2+bx+c,
得: 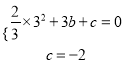 ,∴
,∴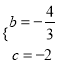 ,
,
∴抛物线的解析式为:y=![]() x2﹣
x2﹣![]() x﹣2;
x﹣2;
(2)设P(m, ![]() m2﹣
m2﹣![]() m﹣2),
m﹣2),
∵PN∥y轴,N在直线AD上,
∴N(m,﹣ ![]() m﹣
m﹣![]() ),
),
∴PN=﹣![]() m﹣
m﹣![]() ﹣
﹣![]() m2+
m2+![]() m+2=﹣
m+2=﹣![]() m2+
m2+![]() m+
m+![]() ,
,
∴当m=![]() 时,PN的最大值是
时,PN的最大值是![]() ;
;
(3)设P(m, ![]() m2﹣
m2﹣![]() m﹣2),
m﹣2),
∵PM∥x轴,M在直线AD上,M与P纵坐标相同,
把y=![]() m2﹣
m2﹣![]() m﹣2,代入y=﹣
m﹣2,代入y=﹣![]() x﹣
x﹣![]() 中,得x=﹣m2+2m+2,
中,得x=﹣m2+2m+2,
∴M(﹣m2+2m+2, ![]() m2﹣
m2﹣![]() m﹣2),
m﹣2),
∴PM=﹣m2+2m+2 -m= ﹣m2+m+2
∴当m=![]() 时,PM的最大值是
时,PM的最大值是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,□OABC的边OC在y轴的正半轴上,OC=3,A(2,1),反比例函数y=
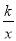 (x>0)的图象经过点B.
(x>0)的图象经过点B.(1)求点B的坐标和反比例函数的关系式;
(2)如图2,将线段OA延长交y=
 (x>0)的图象于点D,过B,D的直线分别交x轴、y轴于E,F两点,①求直线BD的解析式;②求线段ED的长度.
(x>0)的图象于点D,过B,D的直线分别交x轴、y轴于E,F两点,①求直线BD的解析式;②求线段ED的长度. 

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=90°,将△ABC沿AB方向平移AD的长度得到△DEF,已EF=8,BE=3,CG=3,则图中阴影部分的面积是( )
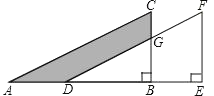
A.12.5B.19.5C.32D.45.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别以Rt△ABC的直角边AC,斜边AB为边向外作等边三角形△ACD和△ABE,F为AB的中点,连接DF,EF,∠ACB=90°,∠ABC=30°.则以下4个结论:①AC⊥DF;②四边形BCDF为平行四边形;③DA+DF=BE;④
 其中,正确的 是( )
其中,正确的 是( )
A.只有①②B.只有①②③C.只有③④D.①②③④
-
科目: 来源: 题型:
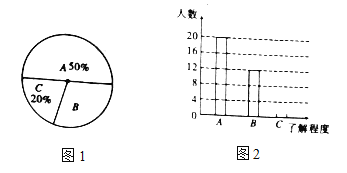
查看答案和解析>>【题目】为传播奥运知识,小刚就本班学生对奥运知识的了解程度进行了一次调查统计:A:熟悉,B:了解较多,C:一般了解图1和图2是他采集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息解答以下问题:
(1)求该班共有多少名学生;
(2)在条形图中,将表示“一般了解”的部分补充完整;
(3)在扇形统计图中,计算出“了解较多”部分所对应的圆心角的度数;
(4)如果全年级共1000名同学,请你估算全年级对奥运知识“了解较多”的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,BC=AC=3,点D是BC边上一点,∠DAC=30°,点E是AD边上一点,CE绕点C逆时针旋转90°得到CF,连接DF,DF的最小值是___.

-
科目: 来源: 题型:
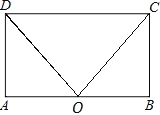
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点O是AB的中点,且OC=OD.
(1)求证:平行四边形ABCD是矩形;
(2)若AD=3,∠COD=60°,求矩形ABCD的面积.
相关试题

