【题目】如图1,□OABC的边OC在y轴的正半轴上,OC=3,A(2,1),反比例函数y=![]() (x>0)的图象经过点B.
(x>0)的图象经过点B.
(1)求点B的坐标和反比例函数的关系式;
(2)如图2,将线段OA延长交y=![]() (x>0)的图象于点D,过B,D的直线分别交x轴、y轴于E,F两点,①求直线BD的解析式;②求线段ED的长度.
(x>0)的图象于点D,过B,D的直线分别交x轴、y轴于E,F两点,①求直线BD的解析式;②求线段ED的长度.


参考答案:
【答案】(1)B(2,4),反比例函数的关系式为y=![]() ;(2)①直线BD的解析式为y=-x+6;②ED=2
;(2)①直线BD的解析式为y=-x+6;②ED=2![]()
【解析】试题分析:(1)过点A作AP⊥x轴于点P,由平行四边形的性质可得BP=4, 可得B(2,4),把点B坐标代入反比例函数解析式中即可;
(2)①先求出直线OA的解析式,和反比例函数解析式联立,解方程组得到点D的坐标,再由待定系数法求得直线BD的解析式; ②先求得点E的坐标,过点D分别作x轴的垂线,垂足为G(4,0),由沟谷定理即可求得ED长度.
试题解析:(1)过点A作AP⊥x轴于点P,
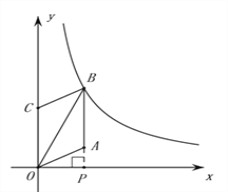
则AP=1,OP=2,
又∵AB=OC=3,
∴B(2,4).,
∵反比例函数y=![]() (x>0)的图象经过的B,
(x>0)的图象经过的B,
∴4=![]() ,
,
∴k=8.
∴反比例函数的关系式为y=![]() ;
;
(2)①由点A(2,1)可得直线OA的解析式为y=![]() x.
x.
解方程组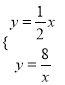 ,得
,得![]() ,
, ![]() .
.
∵点D在第一象限,
∴D(4,2).
由B(2,4),点D(4,2)可得直线BD的解析式为y=-x+6;
②把y=0代入y=-x+6,解得x=6,
∴E(6,0),
过点D分别作x轴的垂线,垂足分别为G,则G(4,0),
由勾股定理可得:ED=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,圆锥底面圆半径为1,母线长为4,图2为其侧面展开图.
(1)求阴影部分面积(π可作为最后结果);
(2)母线SC是一条蜜糖线,一只蚂蚁从A沿着圆锥表面最少需要爬多远才能吃到蜜糖?


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b(k,b为常数,k≠0)的图象与反比例函数
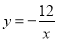 的图象交于A、B两点,且与x轴交于点C,与y轴交于点D,A点的横坐标与B点的纵坐标都是3.
的图象交于A、B两点,且与x轴交于点C,与y轴交于点D,A点的横坐标与B点的纵坐标都是3.(1)求一次函数的表达式;
(2)求△AOB的面积;
(3)写出不等式kx+b>﹣
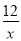 的解集.
的解集.
-
科目: 来源: 题型:
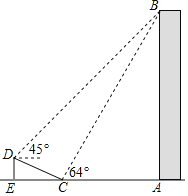
查看答案和解析>>【题目】如图,在大楼AB的正前方有一斜坡CD,CD=13米,坡比DE:EC=1:
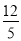 ,高为DE,在斜坡下的点C处测得楼顶B的仰角为64°,在斜坡上的点D处测得楼顶B的仰角为45°,其中A、C、E在同一直线上.
,高为DE,在斜坡下的点C处测得楼顶B的仰角为64°,在斜坡上的点D处测得楼顶B的仰角为45°,其中A、C、E在同一直线上.(1)求斜坡CD的高度DE;
(2)求大楼AB的高度;(参考数据:sin64°≈0.9,tan64°≈2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=90°,将△ABC沿AB方向平移AD的长度得到△DEF,已EF=8,BE=3,CG=3,则图中阴影部分的面积是( )
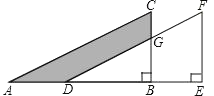
A.12.5B.19.5C.32D.45.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别以Rt△ABC的直角边AC,斜边AB为边向外作等边三角形△ACD和△ABE,F为AB的中点,连接DF,EF,∠ACB=90°,∠ABC=30°.则以下4个结论:①AC⊥DF;②四边形BCDF为平行四边形;③DA+DF=BE;④
 其中,正确的 是( )
其中,正确的 是( )
A.只有①②B.只有①②③C.只有③④D.①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
 x2+bx+c经过点B(3,0)、C(0,﹣2),直线L:y=﹣
x2+bx+c经过点B(3,0)、C(0,﹣2),直线L:y=﹣ x﹣
x﹣ 交y轴于点E,且与抛物线交于A、D两点,P为抛物线上一动点(不与A、D重合).
交y轴于点E,且与抛物线交于A、D两点,P为抛物线上一动点(不与A、D重合).(1)求抛物线的解析式;
(2)当点P在直线L下方时,过点P作PN∥y轴交L于点N,求PN的最大值.
(3)当点P在直线L下方时,过点P作PM∥x轴交L于点M,求PM的最大值.

相关试题

