【题目】如图,已知⊙O中,AB为直径,AB=10 cm,弦AC=6 cm,∠ACB的平分线交⊙O于D , 求BC、AD和BD的长.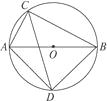
参考答案:
【答案】解:∵AB是直径,∴∠ACB=∠ADB=90°.
在Rt△ACB中,BC= ![]() =
= ![]() =8.
=8.
∵CD平分∠ACB , ∴弧AD=弧BD.∴AD=BD.
在Rt△ADB中,AD=BD= ![]() AB=5
AB=5 ![]() (cm).
(cm).
【解析】∵AB是直径,∴∠ACB=∠ADB=90°.
在Rt△ACB中,BC= ![]() =
= ![]() =8.
=8.
∵CD平分∠ACB,∴弧AD=弧BD.∴AD=BD.
在Rt△ADB中,AD=BD= ![]() AB=5
AB=5 ![]() (cm).
(cm).
【考点精析】掌握勾股定理的概念和圆周角定理是解答本题的根本,需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图24-1-4-16所示,AB是⊙O的直径,C、D、E都是⊙O上的点,则∠1+∠2=.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, △P1OA1与△P2A1A2是等腰直角三角形,点
 、
、 在函数
在函数 的图象上,斜边
的图象上,斜边 、
、 都在
都在 轴上,则点
轴上,则点 的坐标是____________.
的坐标是____________.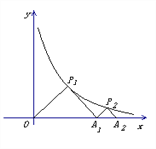
【答案】(
 ,0)
,0)【解析】因为△P1OA1是等腰直角三角形,所以设P1(a,a),则a2=4,a=2,所以OA1=2×2=4,又因为△P2A1A2是等腰直角三角形,设P2(4+b,b),所以b(4+b)=4,解得b=
 ,所以A1A2=
,所以A1A2= ,所以OA2=
,所以OA2= +4=
+4=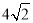 ,则A2(
,则A2( ,0),故答案为(
,0),故答案为( ,0).
,0).【题型】填空题
【结束】
16【题目】如图,函数y=
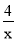 和y=
和y= 在第一象限的图像,点P1,P2,P3,……,P2011都是曲线上的点,它们的横坐标分别为x1,x2,x3,……,x2011,纵坐标分别为1,3,5,7……,是连续的2011个奇数,过各个P点作y的平行线,与另一双曲线交点分别是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),……,Q2012(x2012,y2012),则y2012=___________
在第一象限的图像,点P1,P2,P3,……,P2011都是曲线上的点,它们的横坐标分别为x1,x2,x3,……,x2011,纵坐标分别为1,3,5,7……,是连续的2011个奇数,过各个P点作y的平行线,与另一双曲线交点分别是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),……,Q2012(x2012,y2012),则y2012=___________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,函数y=
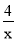 和y=
和y=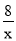 在第一象限的图像,点P1,P2,P3,……,P2011都是曲线上的点,它们的横坐标分别为x1,x2,x3,……,x2011,纵坐标分别为1,3,5,7……,是连续的2011个奇数,过各个P点作y的平行线,与另一双曲线交点分别是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),……,Q2012(x2012,y2012),则y2012=___________
在第一象限的图像,点P1,P2,P3,……,P2011都是曲线上的点,它们的横坐标分别为x1,x2,x3,……,x2011,纵坐标分别为1,3,5,7……,是连续的2011个奇数,过各个P点作y的平行线,与另一双曲线交点分别是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),……,Q2012(x2012,y2012),则y2012=___________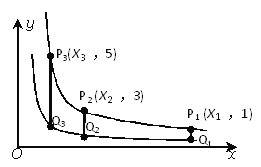
【答案】
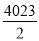
【解析】由题意得,P2012(x2012,4023),因为点P2012在y=
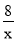 的图象上,所以x2012=
的图象上,所以x2012=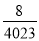 ,把x2012=
,把x2012=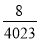 代入 y=
代入 y=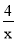 中得y2012=
中得y2012=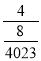 =
=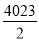 ,故答案为
,故答案为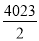 .
.【题型】填空题
【结束】
17【题目】已知y是x的反比例函数,且当x=-4时,y=
 ,
,(1)求这个反比例函数关系式和自变量x的取值范围;
(2)求当x=6时函数y的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上点A表示数a,点B表示数b,点C表示数c,b是最小的正整数,且a,c满足|a+2|+(c-7)2=0.
(1)填空:a=________,b=________,c=________;
(2)画出数轴,并把A,B,C三点表示在数轴上;
(3)P是数轴上任意一点,点P表示的数是x,当PA+PB+PC=10时,x的值为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y是x的反比例函数,且当x=-4时,y=
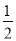 ,
,(1)求这个反比例函数关系式和自变量x的取值范围;
(2)求当x=6时函数y的值.
【答案】(1)
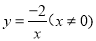 (2)
(2)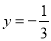
【解析】整体分析:
(1)由反比例函数的这定义求k值,确定x的取值范围;(2)把x=6代入(1)中求得的反比例函数的解析式.
解:(1)设反比例函数关系式为
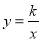 ,
,则k=-4×
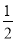 =-2,
=-2,所以个反比例函数关系式是
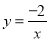 ,自变量x的取值范围是x≠0.
,自变量x的取值范围是x≠0.(2)当x=6时,
 =
=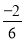 =-
=-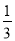 .
.【题型】解答题
【结束】
18【题目】如图,函数y=
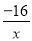 和y= - x+4的图像交点为A、B,原点为O,求△AOB面积.
和y= - x+4的图像交点为A、B,原点为O,求△AOB面积.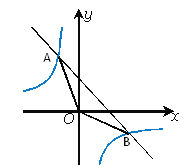
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个3×3的方格中填写了9个数字,使得每行、每列、每条对角线上的三个数之和相等,得到的3×3的方格称为一个三阶幻方.
(1)在图1中空格处填上合适的数字,使它构成一个三阶幻方;
(2)如图2的方格中填写了一些数和字母,当x+y的值为多少时,它能构成一个三阶幻方.

相关试题

